CC的博客

没事就爱瞎折腾

0%

侧信道攻击学习笔记4-利用1个Bit恢复数据

发表于 分类于

简介

  • 本篇将继续跟随chipwhisperer-jupyter sca101的教程来学习从一个Bit的信息来恢复"AES"的密钥，这里的"AES"当然不是标准的AES，但是也挺接近了，为后面能量分析真正的AES提供理论基础

    image-20220820104253537

开始

  • 首先打开Lab 3_2 - Recovering Data from a Single Bit.ipynb，与前面不同，这个notebook不需要硬件就可以完整运行

    image-20220820104552900

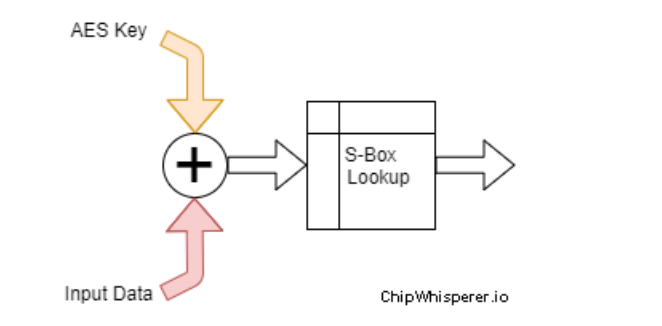
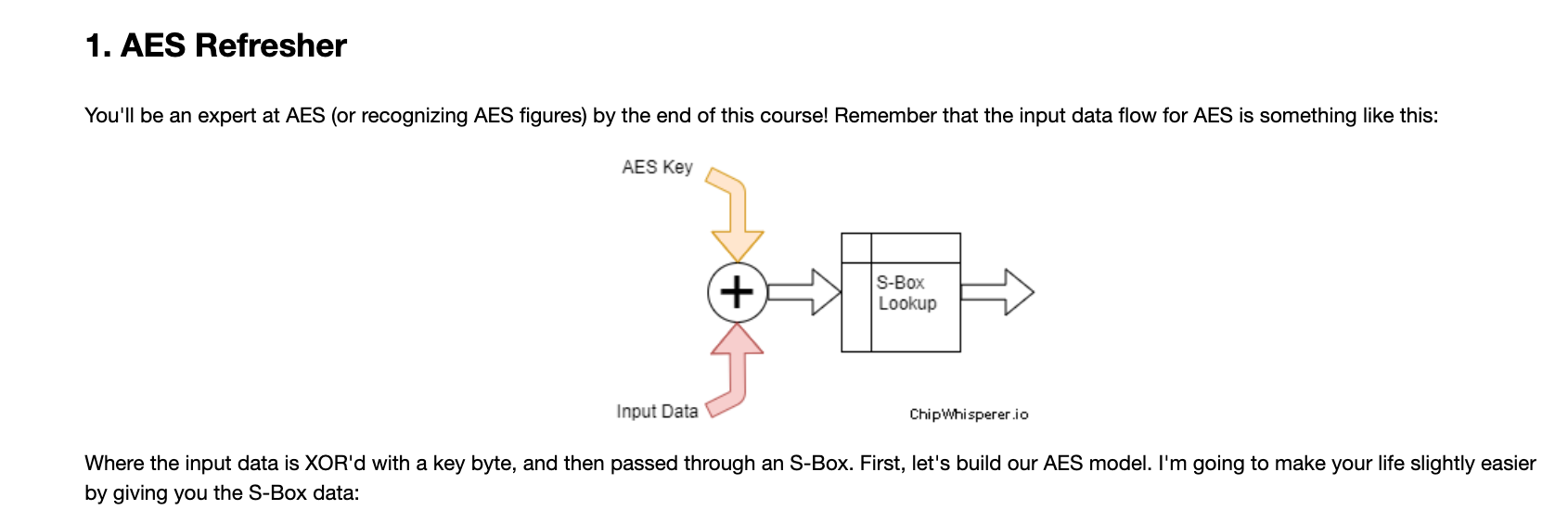
  • 可以到如下提示，大意是说：“你可以把"AES"看成是密钥key和输入数据input异或(XOR)后，再将结果通过S-Box进行字节替换得到输出”。虽然这个"AES"比真正的AES要简单的多，但真正AES的确包含类似的方式，所以通过这个例子来学习确实很适合新手。后面用到的加密模型就是基于下图所提到的XOR + SubBytes

    image-20220820104848010

  • 接着就是给出了AES的S-Box，然后提示根据sbox补全接下来的函数

    image-20220820110342505

  • 补全aes_internal函数，根据提示描述可知实现该函数的要点：1. 输入和输出相异或 2.根据异或结果从sbox中查表获得最后输出，总结起来就是sbox[inputdata ^ key]

    image-20220820110501571

  • 紧接着有个简单检验前面的aes_internal函数是否正确实现的代码块，执行后出现'OK to continue!'就说明应该没什么问题

    image-20220820110811543

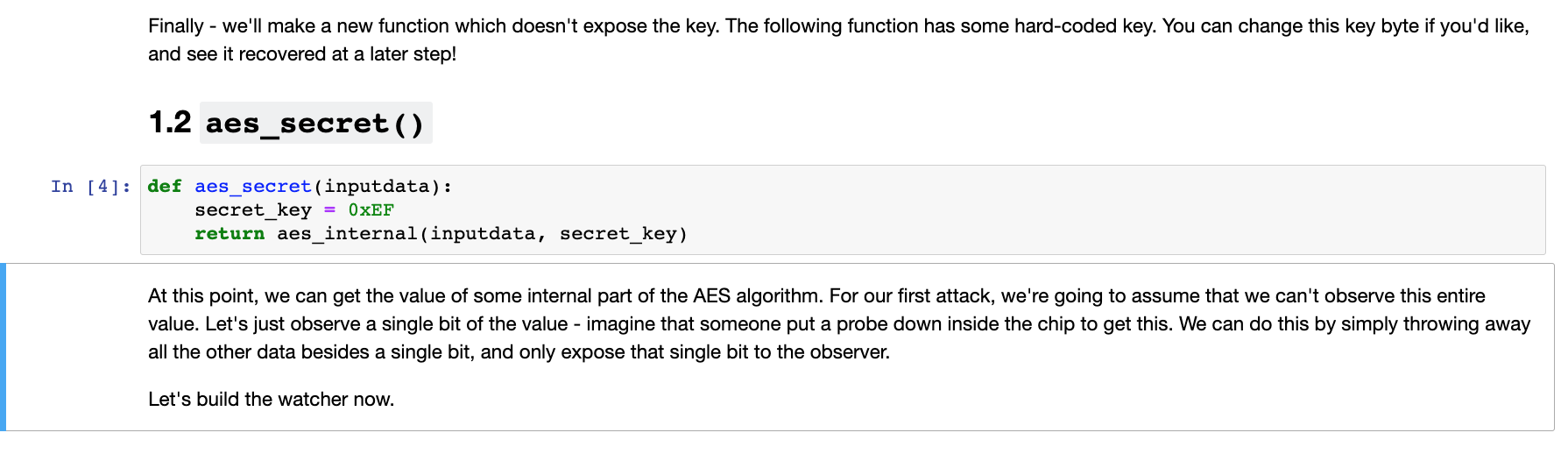
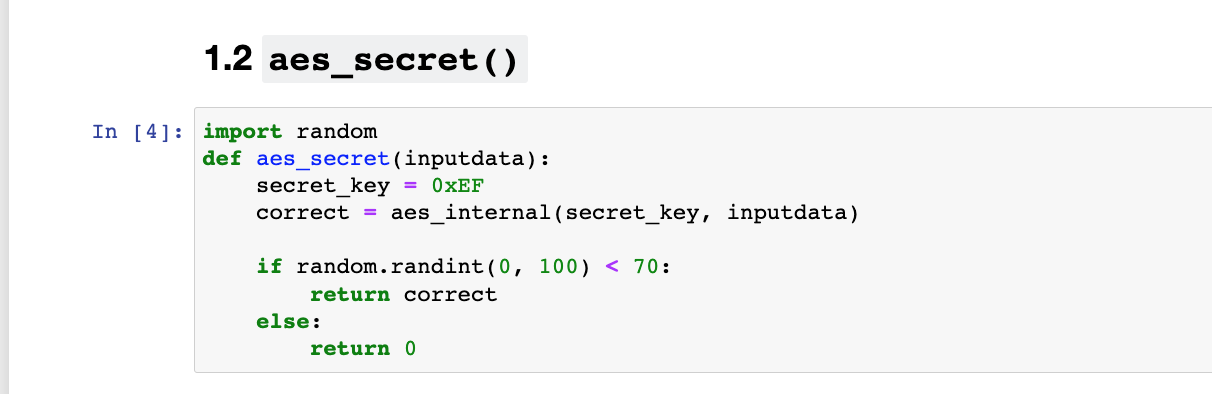
  • 接着可以看到如下提示信息和代码，大意就是：“定义一个新的函数aes_secret，不对外暴露key参数，而是内置一个固定的key。后面的攻击就是攻击这个函数，并且假设我们不能直接获得这个预设的固定key是多少但是能获得1个bit的信息”

​ image-20220820111056601

  • 紧接着看到如下提示信息和代码块，这段信息目的就是通过这个例子引导我们如何用python生成随机数，并将生成数据通过一个加密函数得到输出

    image-20220820112007105

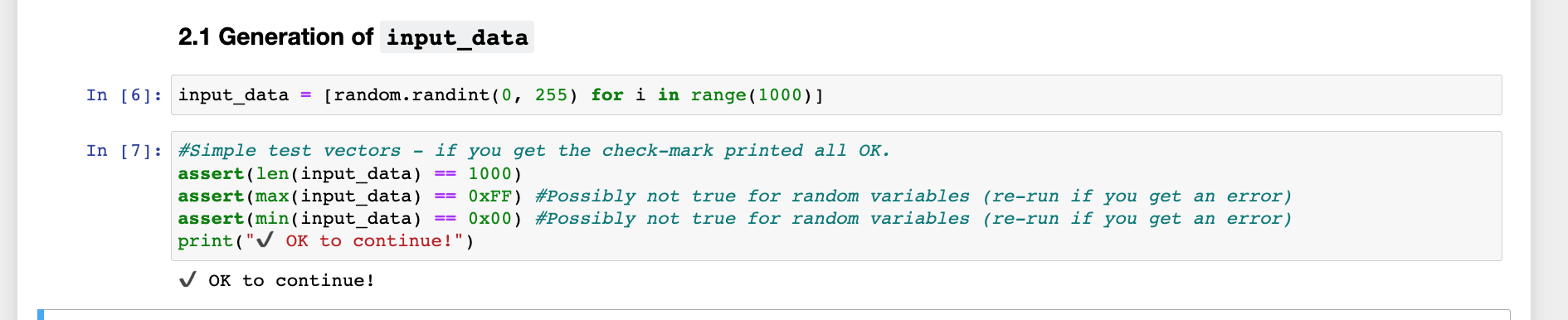
  • 接着就是根据提示，补全生成随机数据input_data的代码，并且同样有一个简单判断代码实现是否正确

    image-20220820112324740

  • 接着是根据提示信息生成泄漏数据（模拟每个byte泄漏一个bit），"& 0x01"的作用就是取最低位，也就是这里取的是每个byte的第0位，另外可以看到，生成的泄漏数据全为'0'和'1'

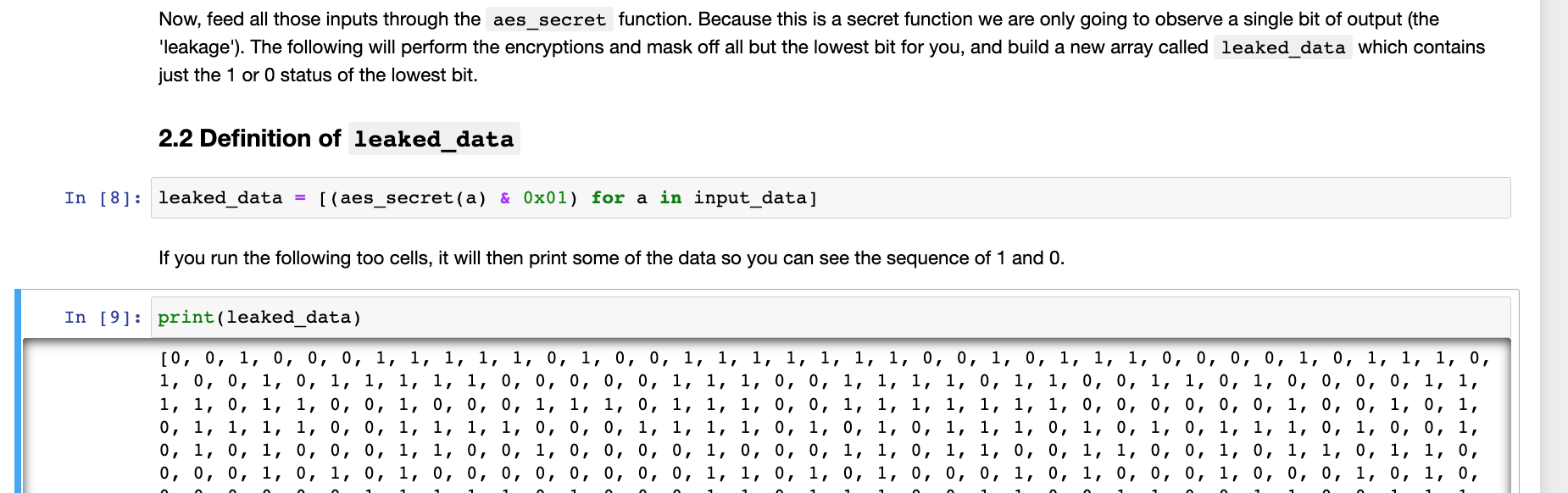
    image-20220820112548952

  • 接着有个提示，可以通过画图来直观查看泄漏数据leaked_data的内容，然后有个提问是：“你认为我们将能从这些数据中获取一些有用的东西吗？让我们攻击它来找到答案”

    image-20220820112959057

  • 接着看到如下提示信息，大意是：“让我们攻击之前的模型（知道算法等信息，只是不知道密钥key），然后用所有可能的key获取一系列的数据，再跟上面泄漏的信息做对比，根据有多少相同来判断猜测是否正确。首先，需要补全一个函数，让该函数返回两个lis之间t有多少相同元素的数量”

    image-20220820140859283

  • 如下图，获得两个list相同元素的数量代码可以用numpy array来实现，先转为numpy array，再让两个array用'=='比较，最后sum就可以计算得到'True'(1)的数量

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    import numpy as np
    def num_same(a, b):
        
        if len(a) != len(b):
            raise ValueError("Arrays must be same length!")

        if max(a) != max(b):
            raise ValueError("Arrays max() should be the same!")
        
        #Count how many list items match up
        _a=np.array(a)
        _b=np.array(b)
        return (_a==_b).sum()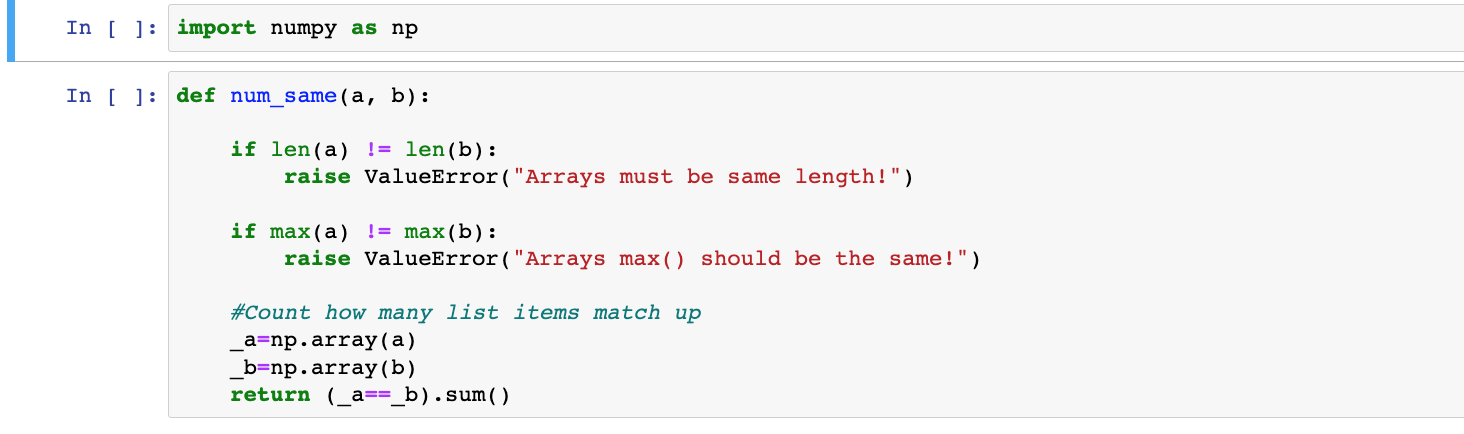

    image-20220820141619791

  • 同样地，有个简单判断我们代码是否正确实现地代码块

    image-20220820141834436

  • 然后可以看到如下提示信息，大意就是：补齐代码，调用aes_internal函数，用key每个可能值[0x00,0x01,...,0xff]加密相同的input_data得到key_guess，再将结果与泄漏数据相比较获得两个list相同的值

    image-20220820141943793

  • 根据上面提示信息可以补全代码，运行结果如下

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    for guess in range(0, 256):   
        
        #Get a hypothetical leakage list - use aes_internal(guess, input_byte) and mask off to only get value of lowest bit
        hypothetical_leakage = [(aes_internal(a,guess) & 0x01) for a in input_data]
        
        #Use our function
        same_count = num_same(hypothetical_leakage, leaked_data)   
        
        #Print for debug
        print("Guess {:02X}: {:4d} bits same".format(guess, same_count))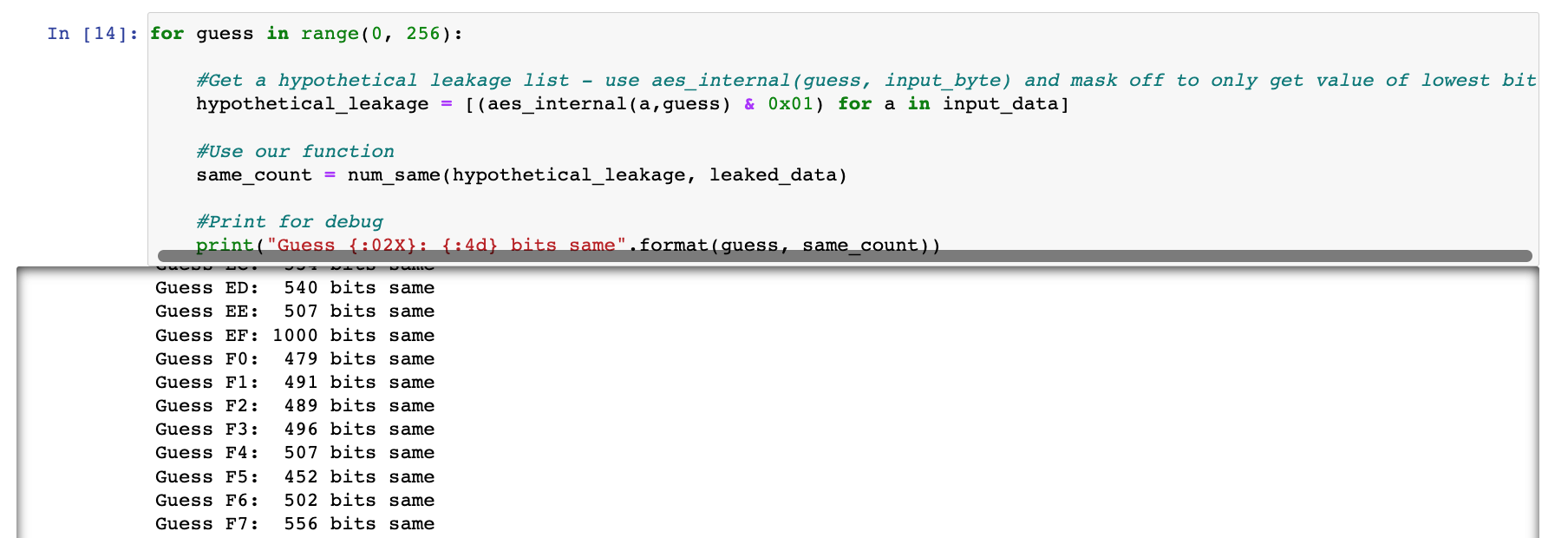

    image-20220820142345382

  • 结合上图的输出信息，正如下图的提示信息一样，大部分猜测的'byte'输出相同数目都是500左右，只有'0xEF'是1000（前提是前面的内置key没有设置为其他），所以'0xEF'是固定密钥key的唯一可能值

    image-20220820142548417

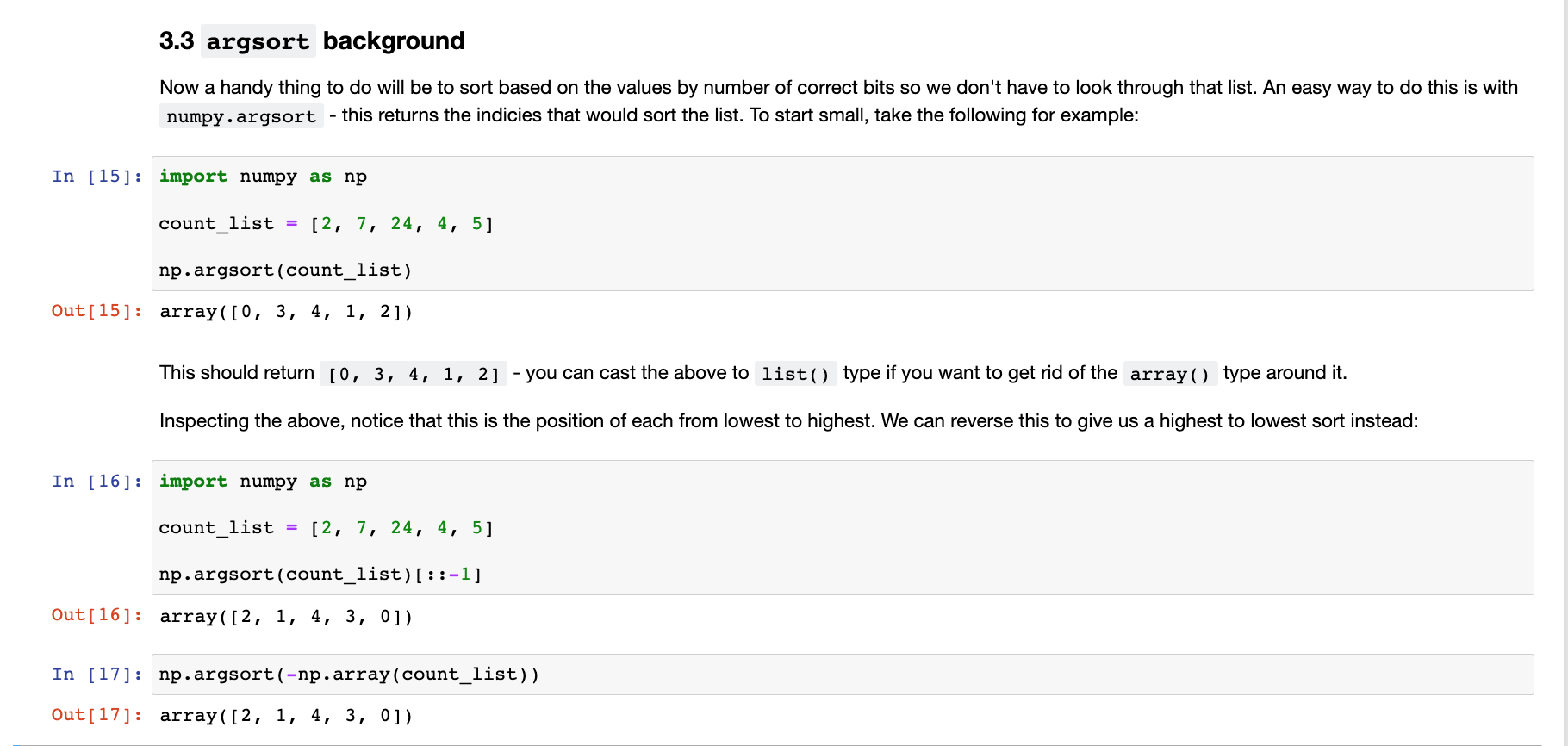
  • 接下来是介绍numpy的argsort，如下图np.argsort()可以从小到大排序一个list（注意这里argsort结果是输出list下标index的排序结果，也就是最小数据所在index到最大数据所在index），要从大到小排序可以在结果加[::-1]或者np.argsort(-np.array(list()))

    image-20220820142841758

  • 接下来的提示信息就是，利用argsort来补全代码，让代码输出相同数前5的猜测key

    image-20220820143458506

  • 按照提示可以补全代码，如下图，可以看到，代码成功输出相同数量排在前5的猜测值

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    import numpy as np

    guess_list = [0] * 256

    for guess in range(0, 256):   
        
        #Get a hypothetical leakage list - use aes_internal(guess, input_byte) and mask off to only get value of lowest bit
        hypothetical_leakage = [(aes_internal(a,guess) & 0x01) for a in input_data]
        
        #Use our function
        same_count = num_same(hypothetical_leakage, leaked_data)   
        
        #Track the number of correct bits
        guess_list[guess] = same_count

    #Use np.argsort to generate a list of indicies from low to high, then [::-1] to reverse the list to get high to low.
    sorted_list = np.argsort(guess_list)[::-1]

    #Print top 5 only
    for guess in sorted_list[0:5]:
            print("Key Guess {:02X} = {:04d} matches".format(guess, guess_list[guess]))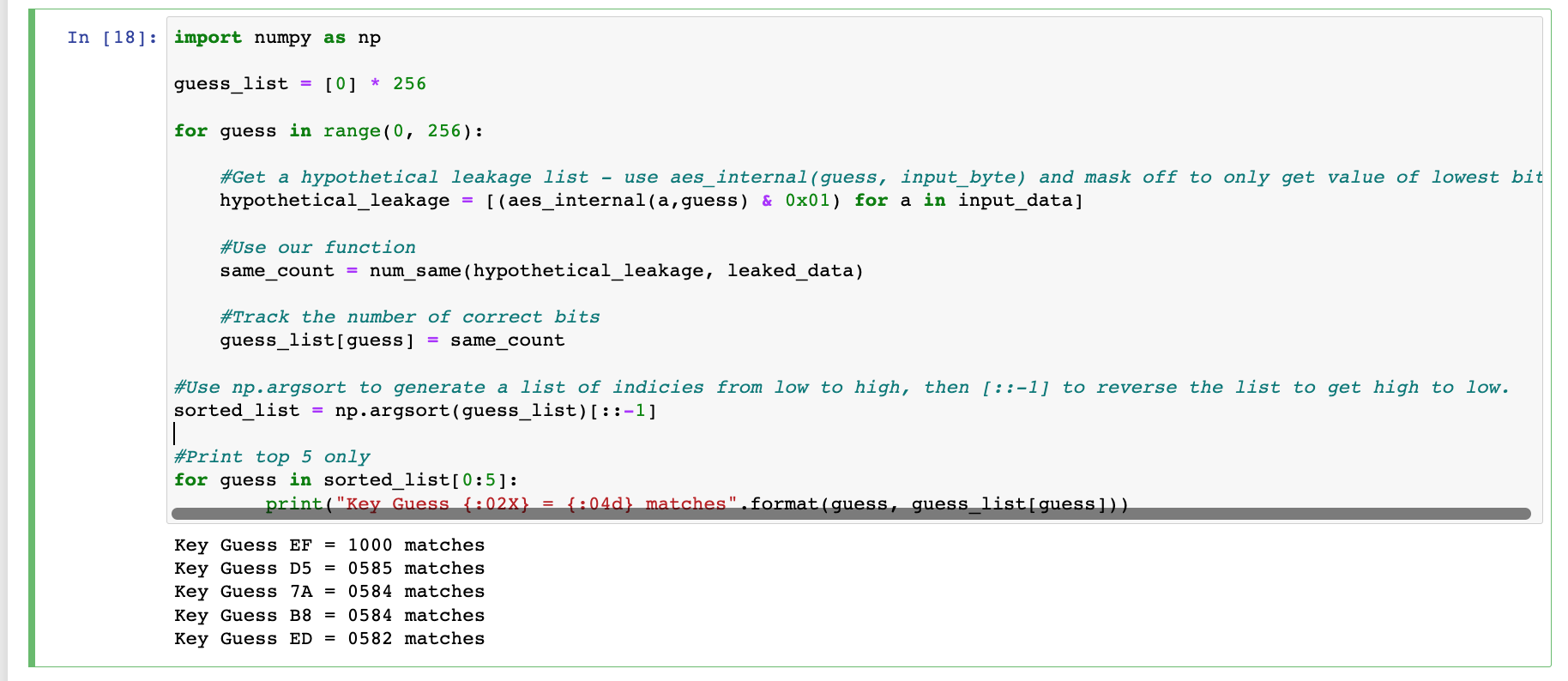

    image-20220820143653346

  • 接下来可以看到如下提示信息，大意是说：“这个例子是我们知道第'0'位就是泄漏数据所在的位，但如果我们不知道泄漏的数据是哪一位信息呢？有个简单的方法解决这个问题就是修改上面的代码让它猜测每个可能byte中8个可能的bit，要做到这点，首先要做的是写一个函数来返回一个byte指定位的值”

    image-20220820143819301

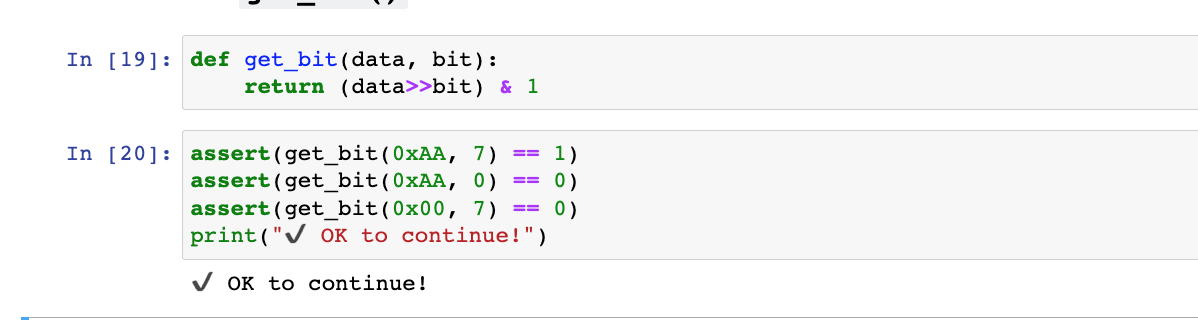
  • 前面可以知道"& 1"可以获得第0位的值，那么获取指定位值就可以配合移位运算来实现。首先将需要获得的位右移到第0位，再用"& 1"即可。如下图get_bit函数如下，同样有个简单判断代码实现是否正确的代码块

    image-20220820144556584

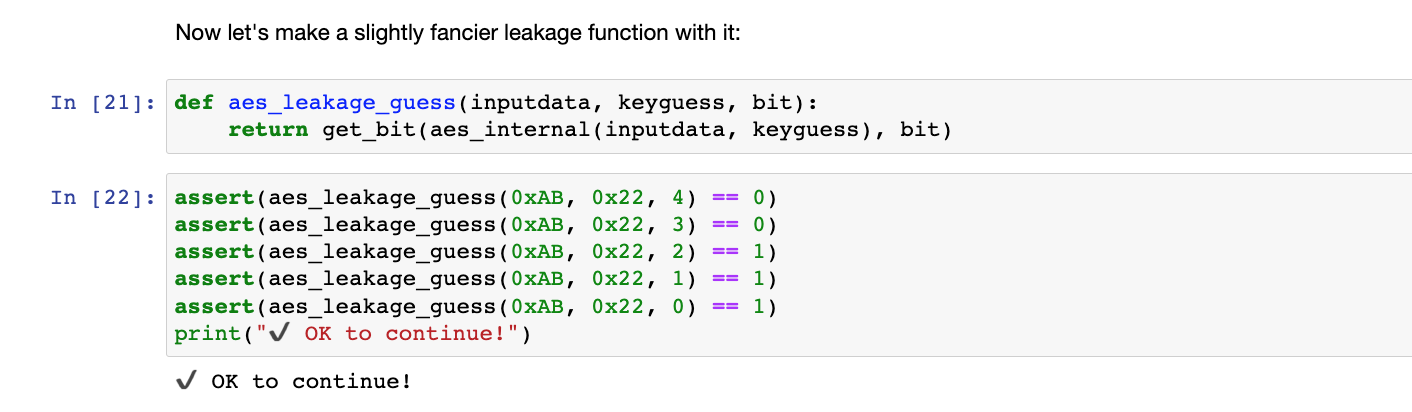
  • 然后就是补全aes_leakage_guess代码

    image-20220820144715156

  • 最后可以看到如下提示信息，大意就是：用上面的aes_leakage_guess函数补全新的循环，获得每个可能byte每个可能的bit与泄漏数据相比相同的数量。而且还提到，将可以看到只有第'0'位的是有'0xEF'=1000，其余位都是500左右的其他结果。

    image-20220820144830653

  • 补全代码如下，结果也确实跟预期一样，只有第0位的才猜测出正确结果

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    for bit_guess in range(0, 8):
        guess_list = [0] * 256
        print("Checking bit {:d}".format(bit_guess))
        for guess in range(0, 256):

            #Get a hypothetical leakage for guessed bit (ensure returns 1/0 only)
            #Use bit_guess as the bit number, guess as the key guess, and data from input_data
            hypothetical_leakage = [aes_leakage_guess(a, guess, bit_guess) for a in input_data]

            #Use our function
            same_count = num_same(hypothetical_leakage, leaked_data)   

            #Track the number of correct bits
            guess_list[guess] = same_count

        sorted_list = np.argsort(guess_list)[::-1]

        #Print top 5 only
        for guess in sorted_list[0:5]:
                print("Key Guess {:02X} = {:04d} matches".format(guess, guess_list[guess]))

    image-20220820145249765

  • 修改前面的leaked_data的代码，可以按如下图修改，这样泄漏数据就是第'3'位的泄漏数据了

    image-20220820145518040

  • 重新往下运行，可以看到变成第'3'位猜测才有1000 matches了，与预期一致

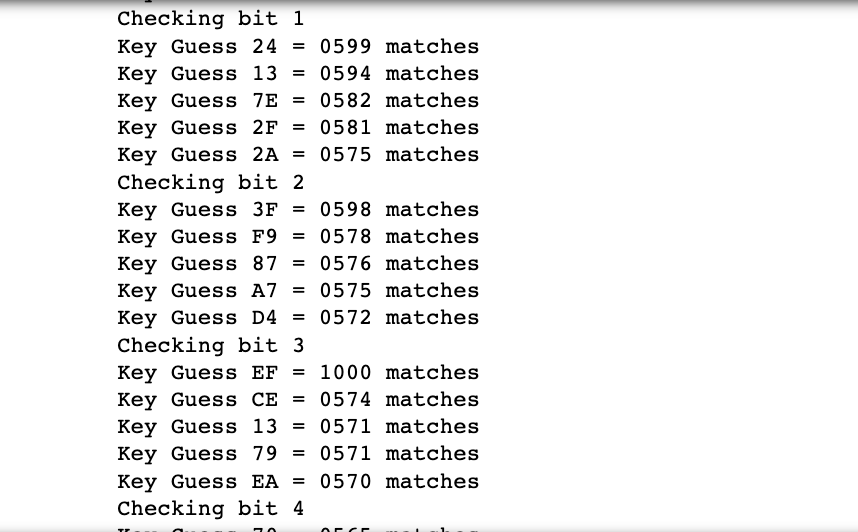
    image-20220820145740656

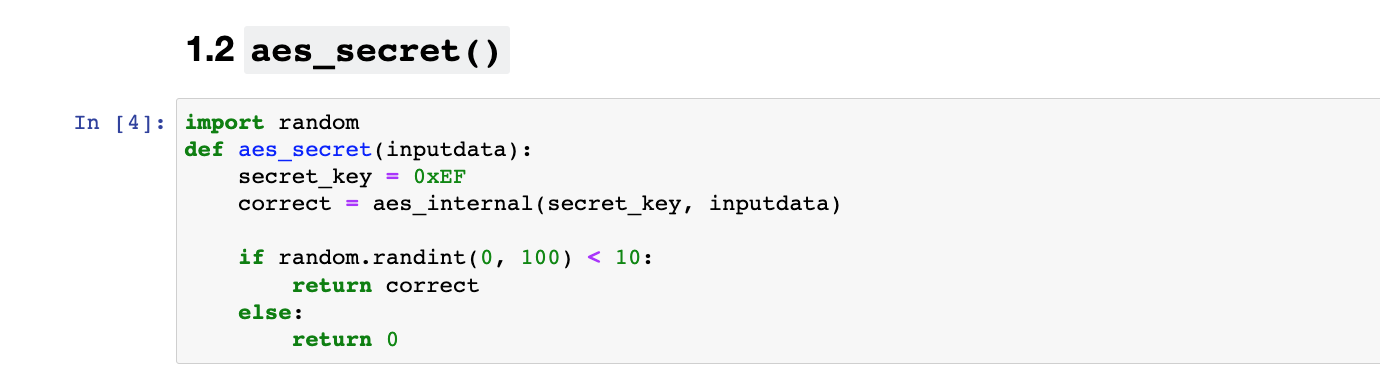
  • 接下来，可以看到如下提示信息，大意就是：给泄漏数据的函数加点“料”，修改aes_secret函数，让它根据随机数来决定返回正确加密结果还是0，以此来模拟噪声

    image-20220820145907896

  • 然后可以看到如下提示信息，大意就是：加料后会发生什么？-会影响猜测的key的准确率，而且事实上，将返回正确加密后的值的概率和需要多少观察数据来恢复正确的key画图，可以得到如下图所示的结果，从图可知70%以上正确率的基本上都只需要少量数据就可以恢复出正确的key。

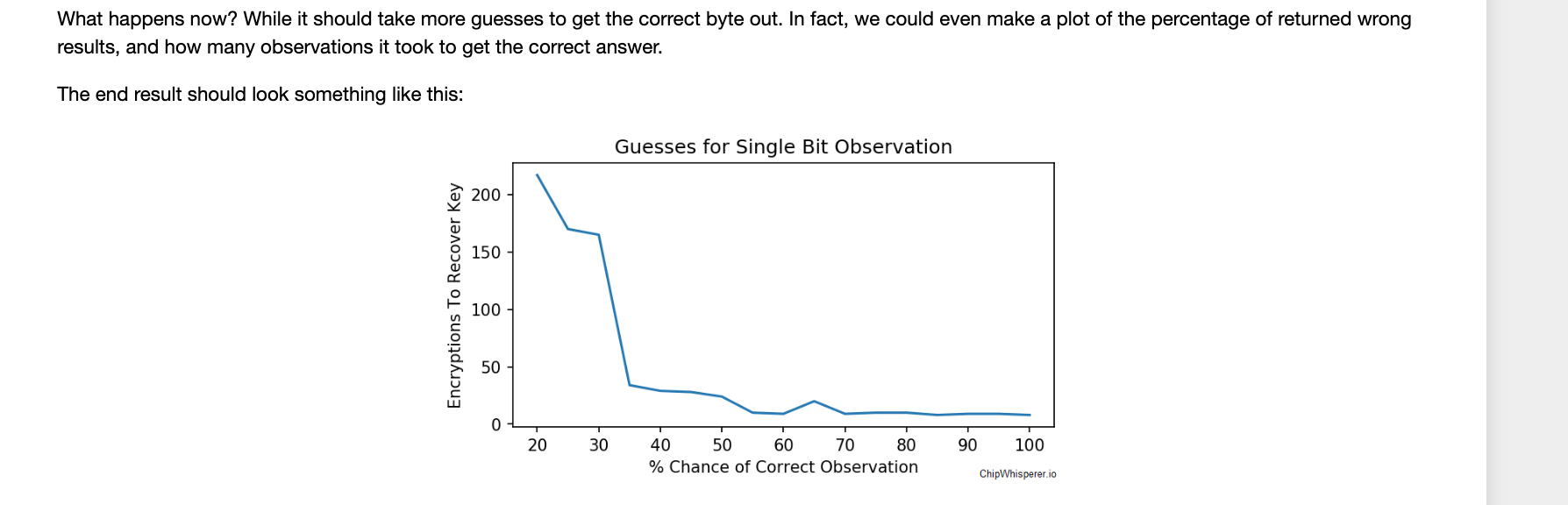
    image-20220820150106933

  • 接下来测试下，让aes_secret有70%概率返回正确结果，并且为了避免混淆，将leaked_data重新改为，获取第'0'位的数据

    image-20220820151437119

    image-20220820150909975

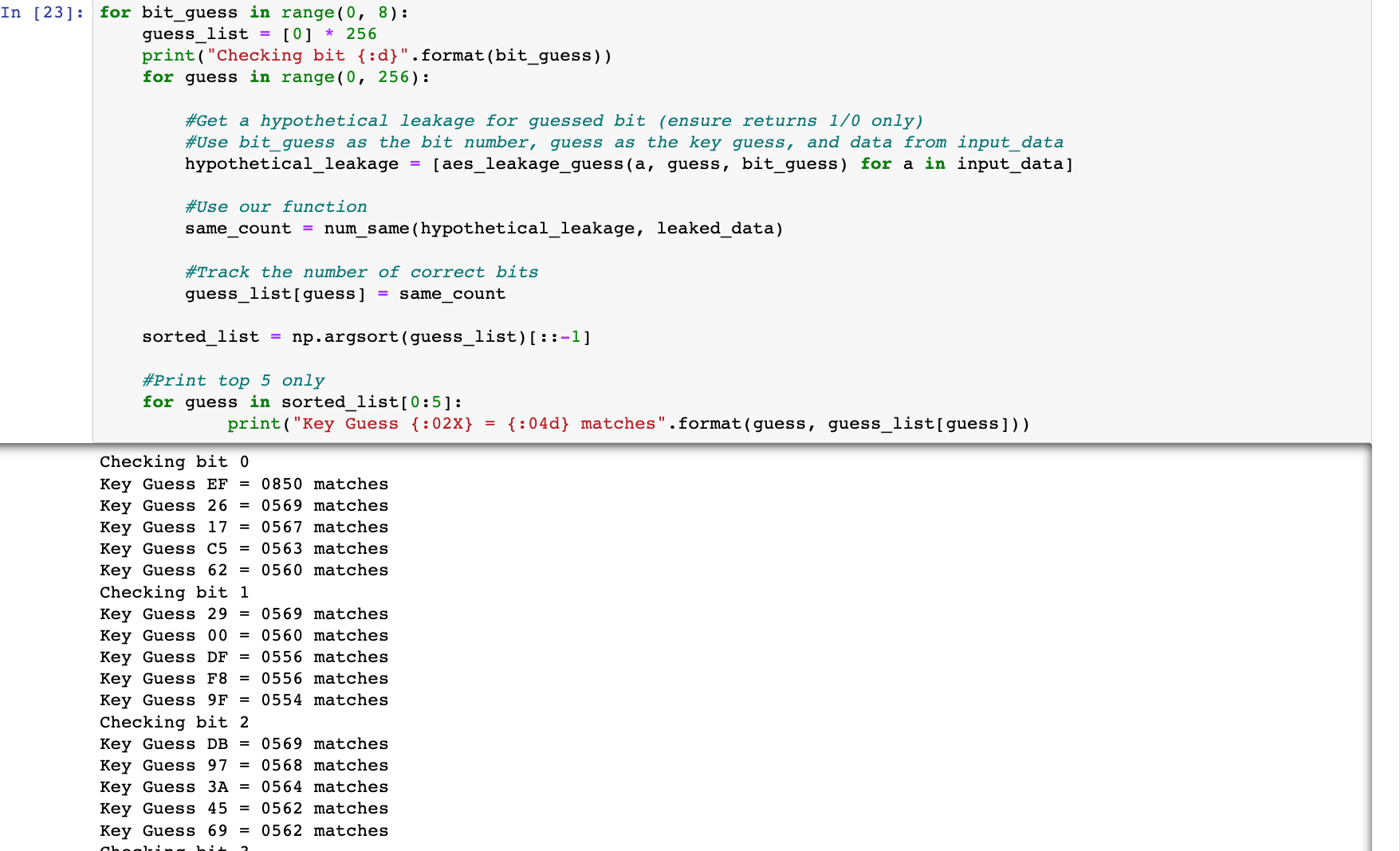
  • 最后结果如下图所示：可以看到，虽然同样可以得到正确的'0xEF'，但是matches值已经变小了很多，但是与其他相比还是有明显的大小区别

    image-20220820151505947

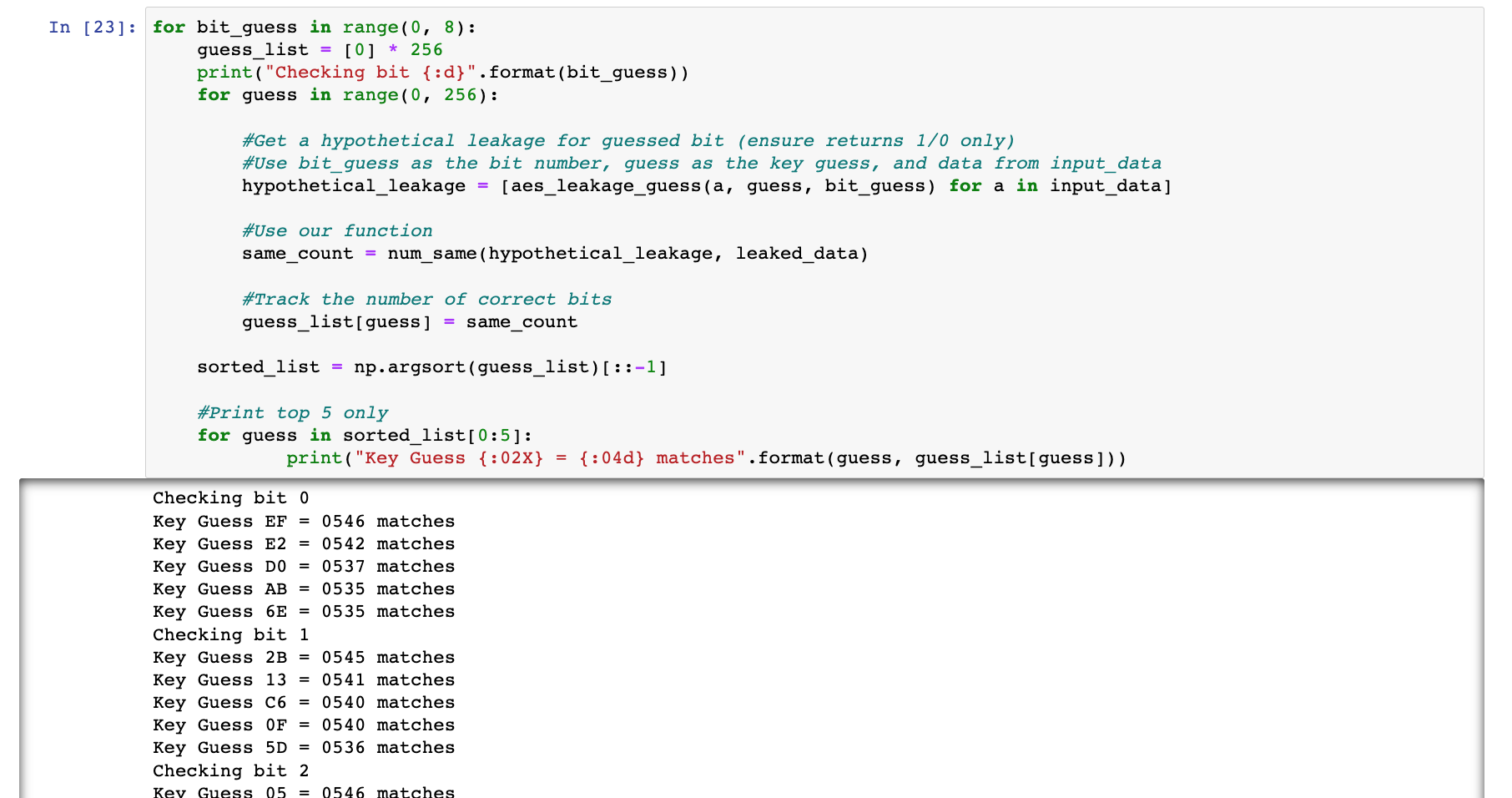
  • 再来看看10%正确返回的结果，可以看到，虽然同样排在第一的是'0xEF'，但是'0xEF'对应的matches数量与排在第2位的0x'E2'差异不大，所以不能只通过一组数据来确定正确密钥是'0xEF'

    image-20220820151621619

    image-20220820151658074

总结

  • 学习了如何利用一位的泄漏数据来恢复"AES"的密钥
  • 在实际情况中因为存在噪声等因素地干扰，往往需要更多地数据才能正确恢复密钥