简介
本篇将继续跟随chipwhisperer-jupyter sca101的教程来学习比差分能量分析(Differential Power Analysis, DPA)更强大的相关性能量分析(Correlation Power Analysis, CPA)
在之前的DPA学习中为了恢复完整的AES密钥,需要抓取了大量的能量迹(几千条),而这里使用CPA只需要50条能量迹即可恢复完整的AES密钥,如此足矣可见这个方法的强大之处
开始
老规矩,将硬件的部分复制到MAIN中执行

抓取50条能量迹,如果是NANO则需要200条

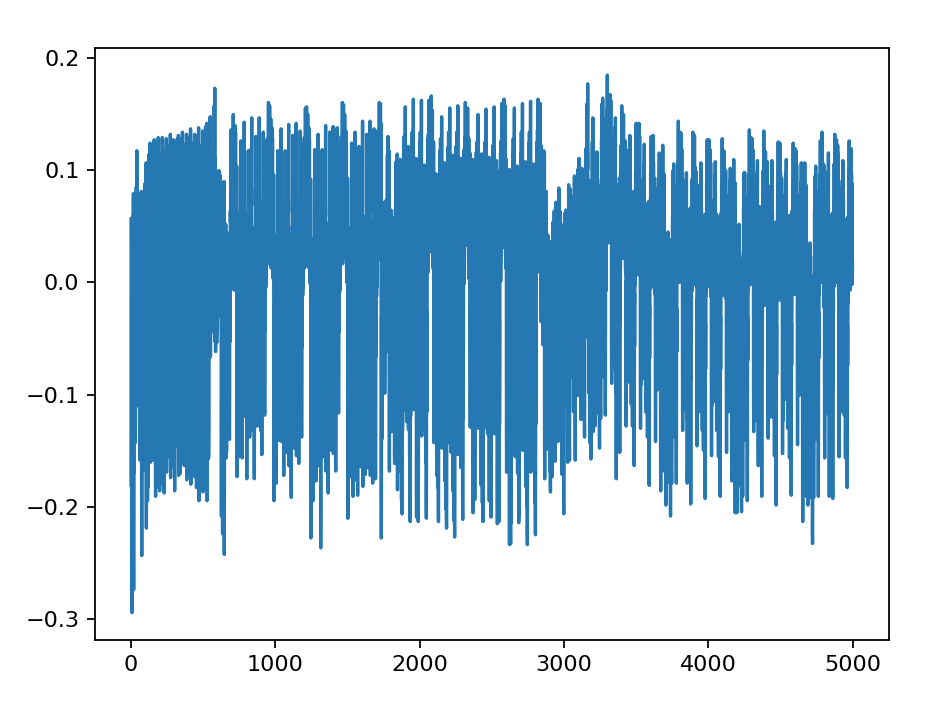
画出单条能量迹,应该可以看到形如下图的峰形
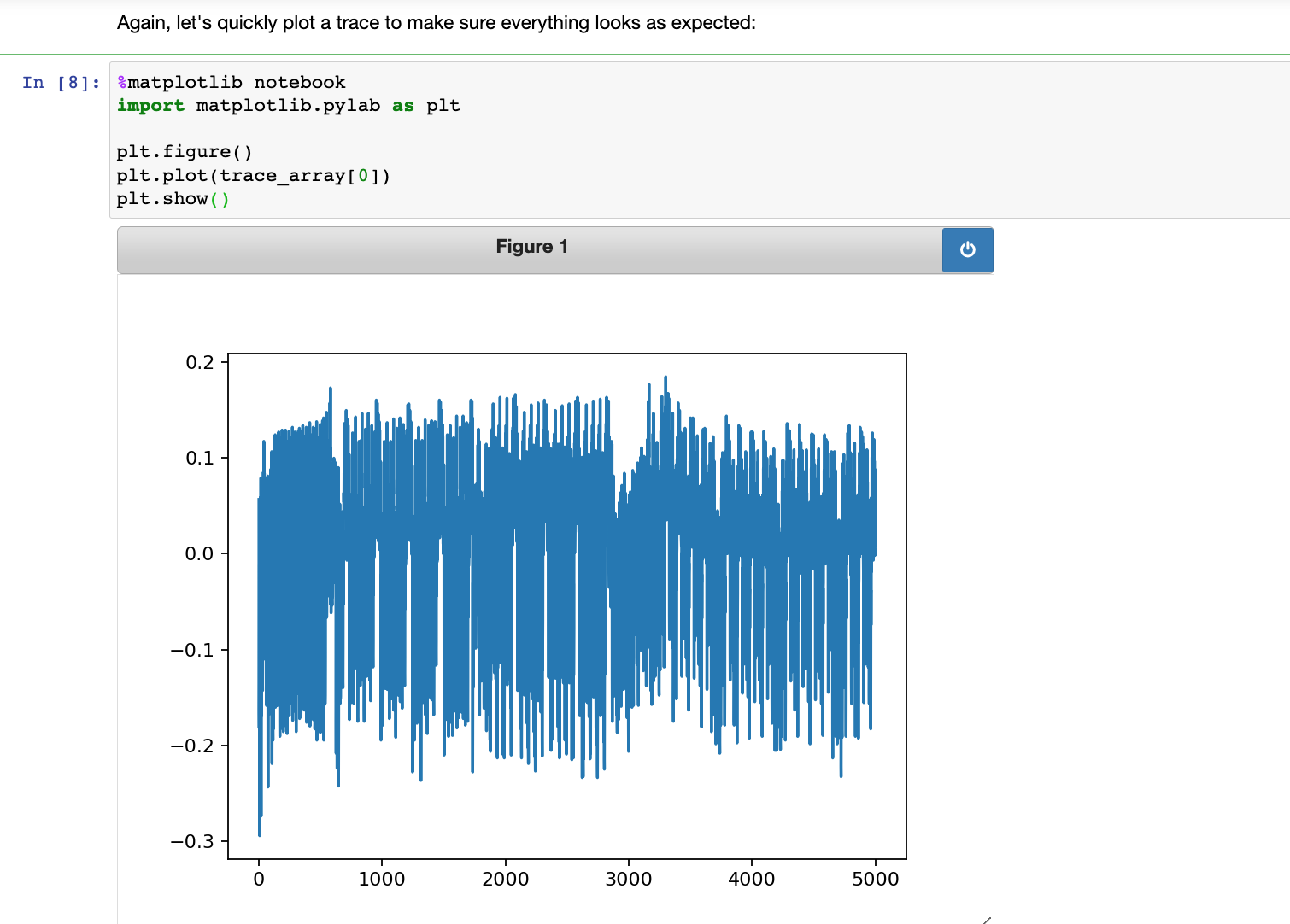
这里提示我们复制前几篇用到的AES模型代码和计算Hamming Weight的代码

按照提示,复制并运行即可
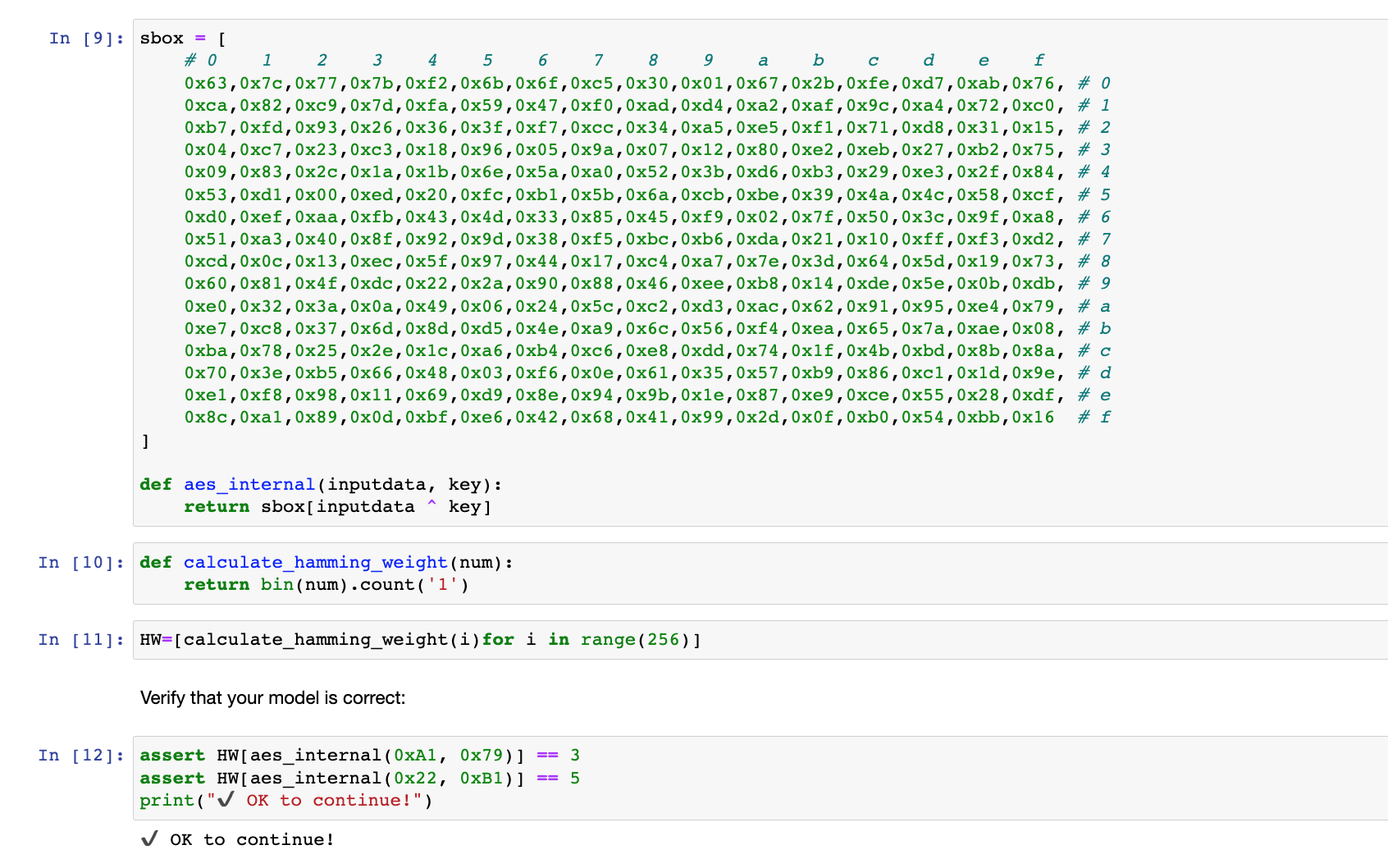
接下来的提示是我们开发自己的相关系数算法(虽然有很多库可以直接计算,但是用代码实现数学算法是一个实用的技能)

对于长度为N的数据集X和Y,其相关系数的计算公式为$$r = \frac{cov(X, Y)}{\sigma_X \sigma_Y}$$
$cov(X, Y)$ 为X和Y的协方差,可按以下公式计算:
$$cov(X, Y) = \sum_{n=1}^{N}[(Y_n - \bar{Y})(X_n - \bar{X})]$$
$\sigma_X$ 和 $\sigma_Y$ 为两个数据集的标准差,可按以下公式计算:
$$\sigma_X = \sqrt{\sum_{n=1}^{N}(X_n - \bar{X})^2}$$
为了实现代码计算相关系数,首先可以分模块实现,如:实现计算平均值的函数mean、实现计算标准差的函数std_dev、实现计算协方差函数cov。可以用**
np.sum(X, axis=0)**来替换所有求和符号$\sum$按照提示,可以实现以下3个函数

接着运行检查函数,查看mean、std_dev、cov三个函数是否正确实现
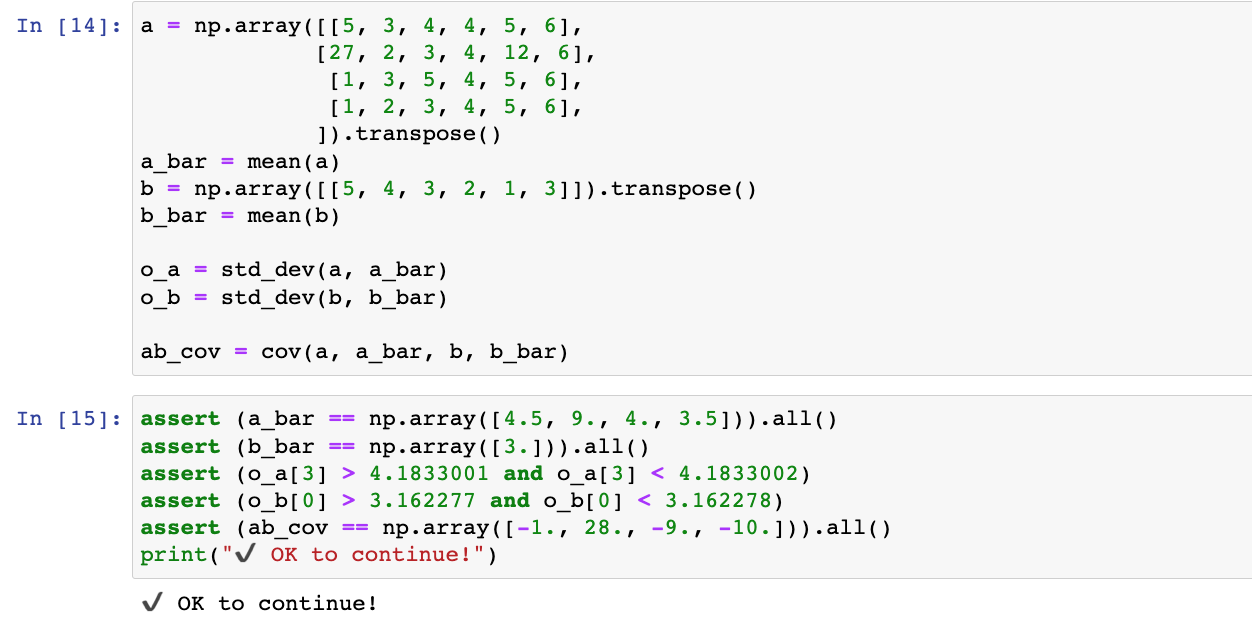
紧接着往下运行可以看到很多提示信息

根据提示,补全代码后运行,可以看到AES密钥第一个字节的猜测结果为"0x2b",相关系数为0.82
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20maxcpa = [0] * 256
# we don't need to redo the mean and std dev calculations
# for each key guess
t_bar = mean(trace_array)
o_t = std_dev(trace_array, t_bar)
for kguess in range(0, 256):
hws = np.array([[HW[aes_internal(textin[0],kguess)] for textin in textin_array]]).transpose()
hw_bar = mean(hws)
o_hw = std_dev(hws, hw_bar)
hw_cov = cov(trace_array,t_bar, hws, hw_bar)
cpaoutput = hw_cov/(o_t*o_hw)
maxcpa[kguess] = max(abs(cpaoutput))
guess=np.argmax(maxcpa)
guess_corr=maxcpa[guess]
print("Key guess: ", hex(guess))
print("Correlation: ", guess_corr)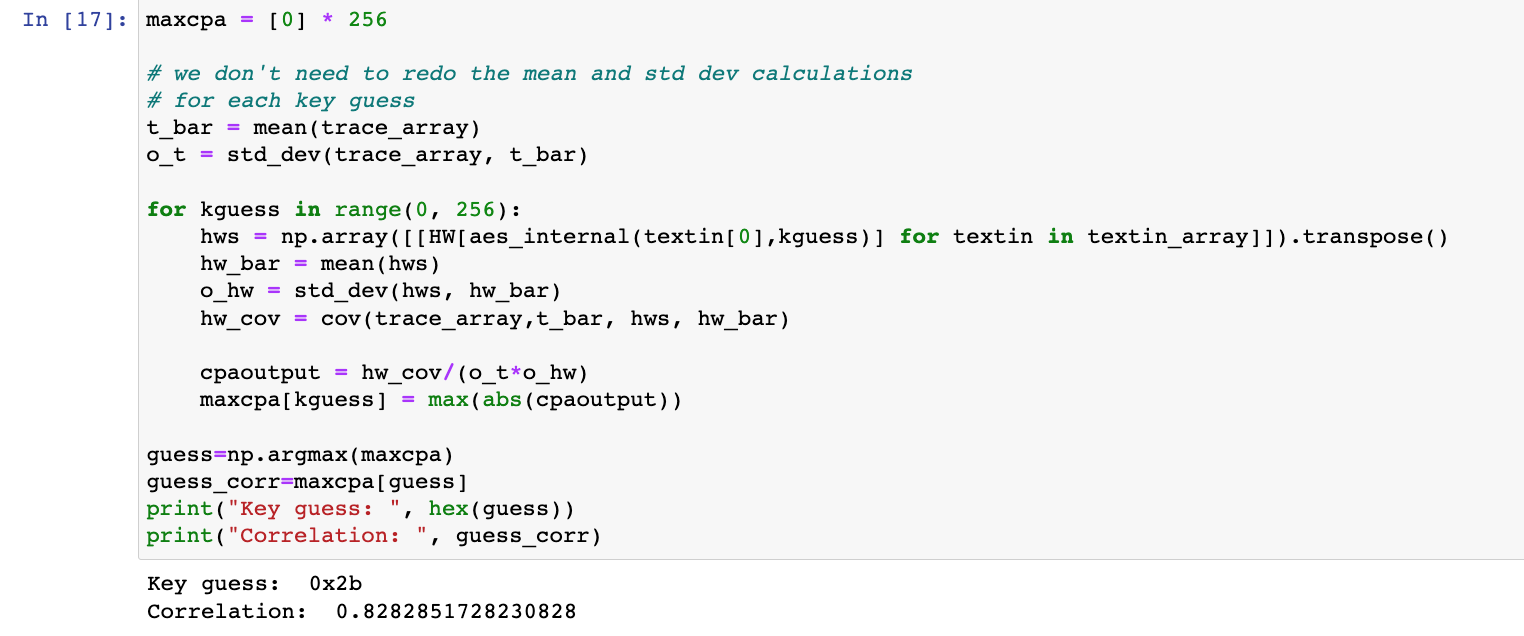
如下图,可以看到,有个判断是否正确猜测AES密钥第一个字节的代码块,"0x2b"为实际AES密钥的第一个字节

接着根据提示补全代码,自动判断AES密钥所有16个字节
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25t_bar = np.sum(trace_array, axis=0)/len(trace_array)
o_t = np.sqrt(np.sum((trace_array - t_bar)**2, axis=0))
cparefs = [0] * 16 #put your key byte guess correlations here
bestguess = [0] * 16 #put your key byte guesses here
for bnum in range(0, 16):
maxcpa = [0] * 256
for kguess in range(0, 256):
hws = np.array([[HW[aes_internal(textin[bnum],kguess)] for textin in textin_array]]).transpose()
hw_bar = mean(hws)
o_hw = std_dev(hws, hw_bar)
hw_cov = cov(trace_array,t_bar, hws, hw_bar)
cpaoutput = hw_cov/(o_t*o_hw)
maxcpa[kguess] = max(abs(cpaoutput))
guess=np.argmax(maxcpa)
guess_corr=maxcpa[guess]
bestguess[bnum]=guess
cparefs[bnum]=guess_corr
print("Best Key Guess: ", end="")
for b in bestguess: print("%02x " % b, end="")
print("\n", cparefs)运行结果如下图所示,使用CPA成功恢复了完整的AES密钥"2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c"

最后可以看到如下提示信息,大意是有个新公式可以用来实时的计算更新相关系数,这个方法会在下一个教程中使用

总结
- 学习了如何简单用python代码实现相关系数的计算
- 学习了如何利用相关系数能量分析和少量能量迹来恢复AES密钥