侧信道攻击学习笔记5-差分能量分析攻击固件中的AES实现

简介

本篇将跟随chipwhisperer-jupyter sca101的教程来学习DPA(Differential Power Analysis，差分能量分析)
与上一篇不同，本篇将攻击真正的AES算法

开始

这次选择的是Lab3_3，可以看到同样有MAIN、HARDWARE和SIMULATED三种ipynb，这里同样选择将硬件的内容复制到MAIN中执行
首先可以看到选择版本号的提示如下图所示，这里提到对于'CWLITEXMEGA'的加密模块可以选择'AVRCRYPTOLIB'，但这里不选择'AVRCRYPTOLIB'，因为测试选用这个，效果太好了，可以相对比较轻松的恢复整个AES密钥，基于学习目的，所以这里保持默认，选择'TINYAES128C'
前几行代码，跟之前的作用一样，初始化chipwhisperer，编译目标板固件并上传
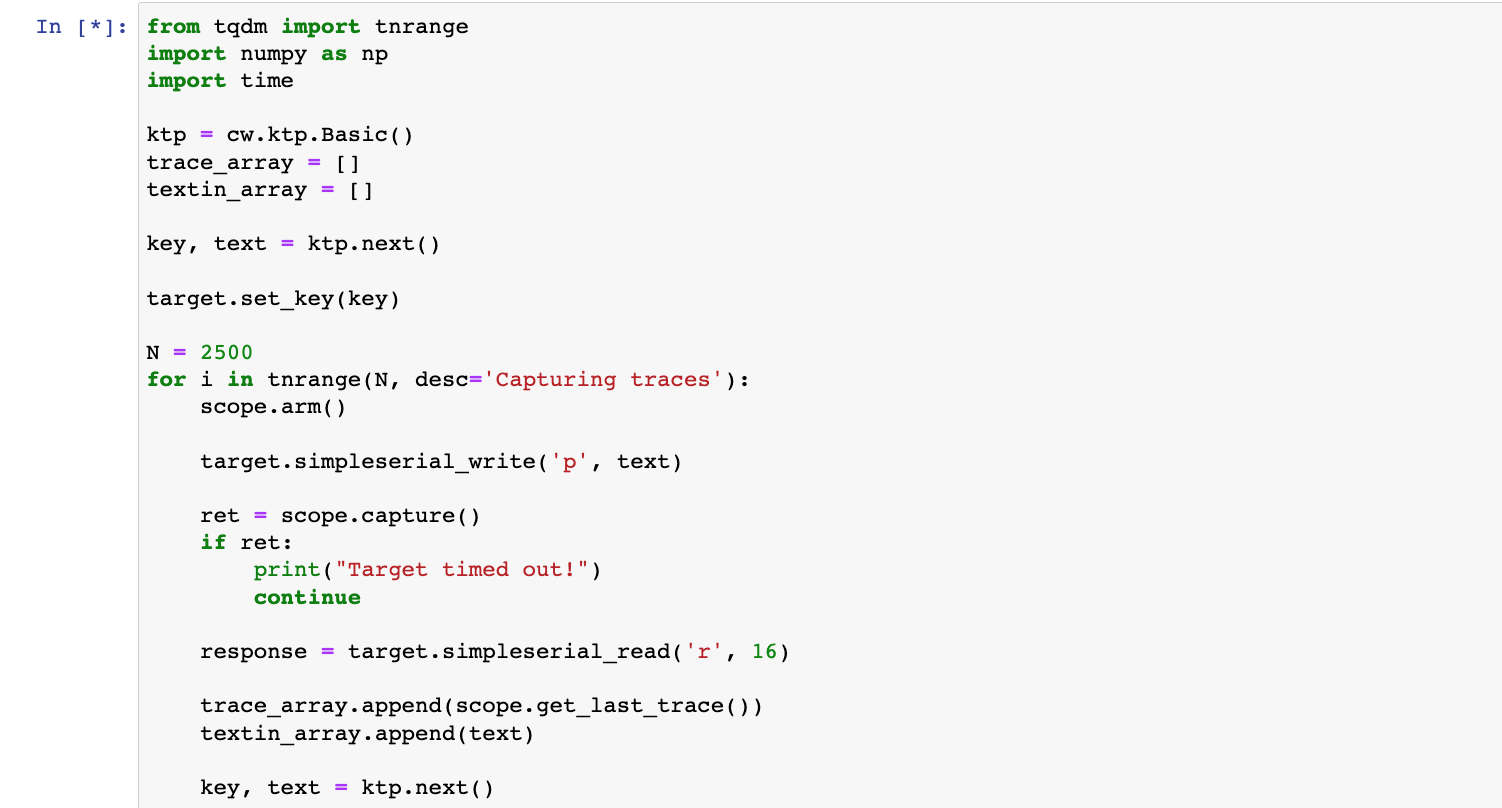
接下来的代码，就是抓取2500条能量迹
接下来查看MAIN中的Summary，大意是：“在上一个的教程中，你知道了如何利用一个位的信息去恢复一个AES密钥的byte。需要注意的是，这个方法之所以能生效是因为我们攻击的数据流中存在那个S-Box。接下来我们将学习如何用能量分析而不是一个实际的bit去恢复AES密钥。这项技术的目标是利用S-Box输出结果的一个bit（无论哪个bit都行）将能量迹分成两部分。如果那个bit的值是1，那么对应的那组数据的能耗将比另一组的要高。这些都基于之前的教程：数据总线中数据的值与能量消耗之间有一定的联系”
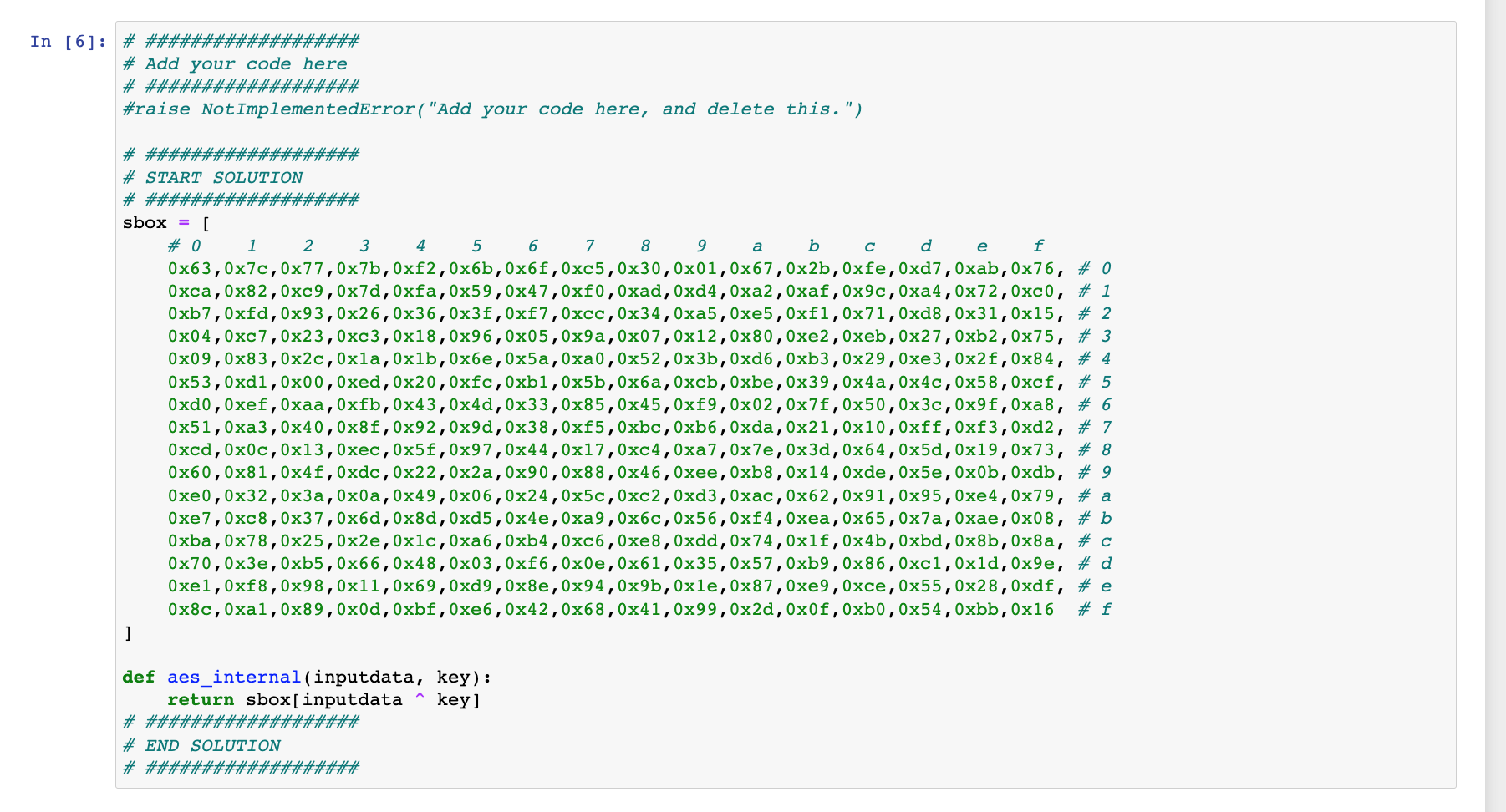
接下来看到如下提示，大意是说：“不需要记住AES复杂的模型-我们可以直接将上一篇的AES模型复制过来”
如下图，这部分代码确实是上一篇中的AES简单模型。这里之所以能用这个模型是因为，真正的AES模型也包含了这个流程，只是多了其它几个流程。DPA分析AES时，不需要知道这个流程具体发生在能量迹的哪个时间点，但是整个能量迹的时间段需要包含这个流程发生的时间段，不然就无法分析（都没抓取到，当然无法分析）。
接下来的提示，是说完成生成能量迹的代码，可以选择模拟或者硬件的代码复制过来。这里上面已经复制了硬件的代码运行了，所以直接跳过到下一个节点
往下掉提示是完成画图的代码，画出一到两条能量迹
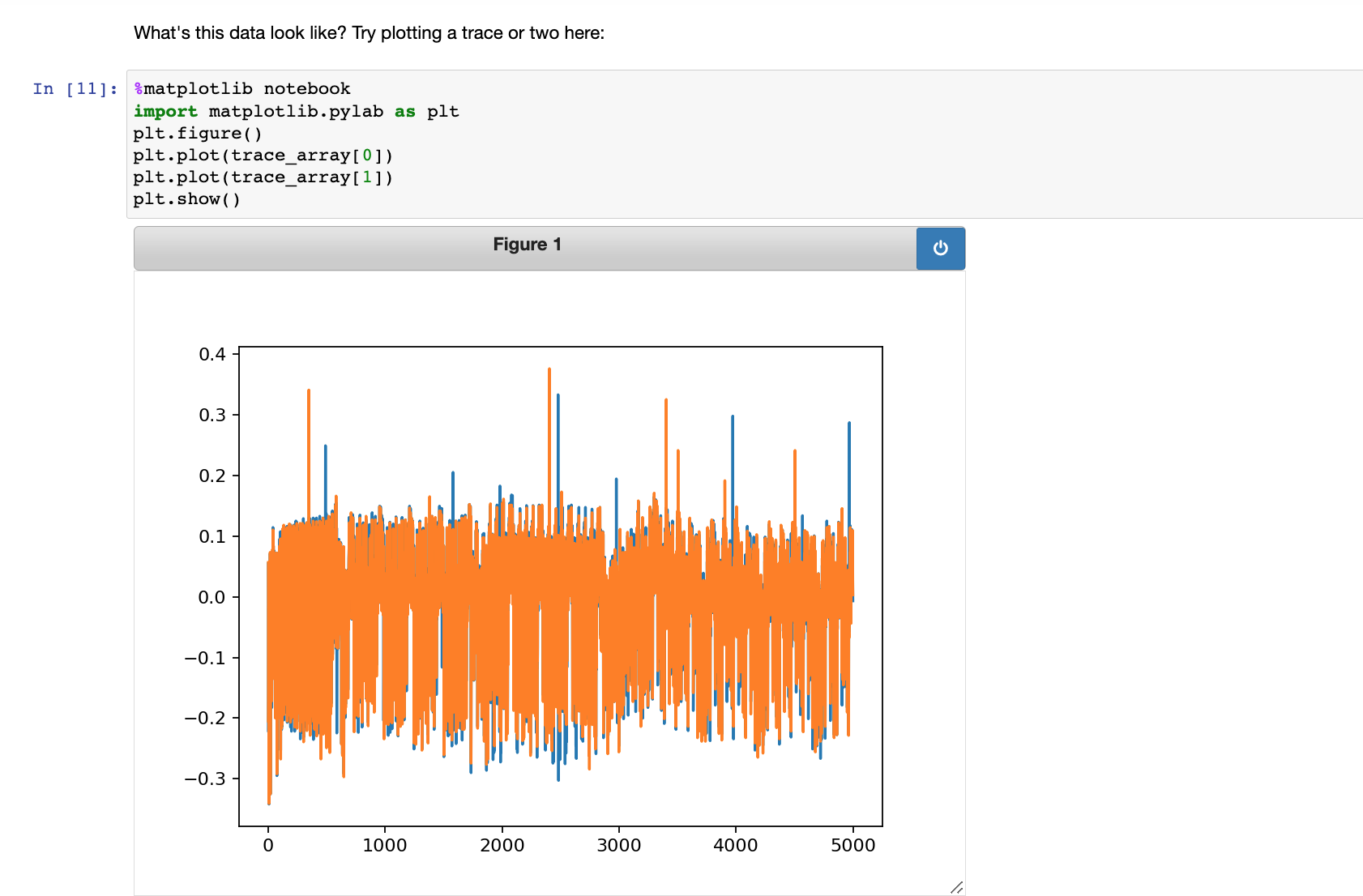
接着是查看输入数据是什么样的
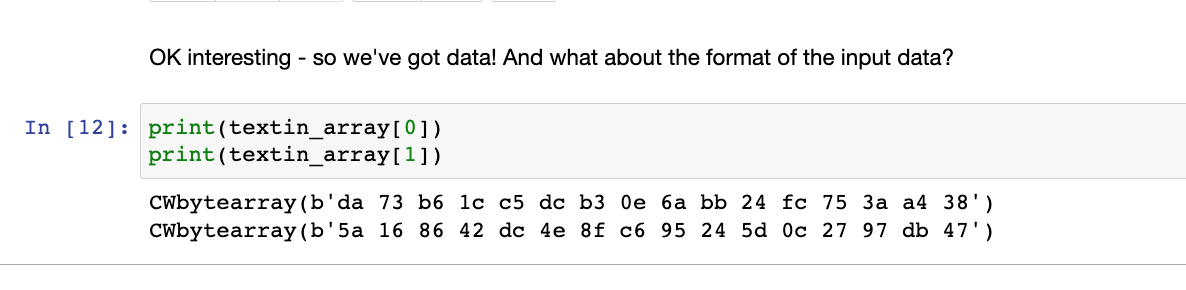
接下来的提示是说：这个攻击需要用一个方法将能量迹分成两组，分组的依据是我们猜测的值中的一个bit。这里为了简单起见，先猜测一个byte的AES密钥。开始之前-需要定义能量迹的数量和每条能量迹的点的数量。可以直接运行下面的代码例子来定义这两个变量
接下来的提示信息，大意是：让我们补全代码，将能量迹分成两组，并将两组求平均值，再取两者差的绝对值，最后得到两组中的最大差值。有个需要注意的是使用numpy的mean计算平均值时，需要指定axis=0。为了方便测试，还给出了密钥key第一个byte的真实值0x2b。如果遇到问题，往后还有提示。
根据上面信息补全代码，运行后如下图所示，可以看到只有0x2b拥有最大的差异值，与上面描述的一致，这样就恢复了key的第一个byte："0x2b"
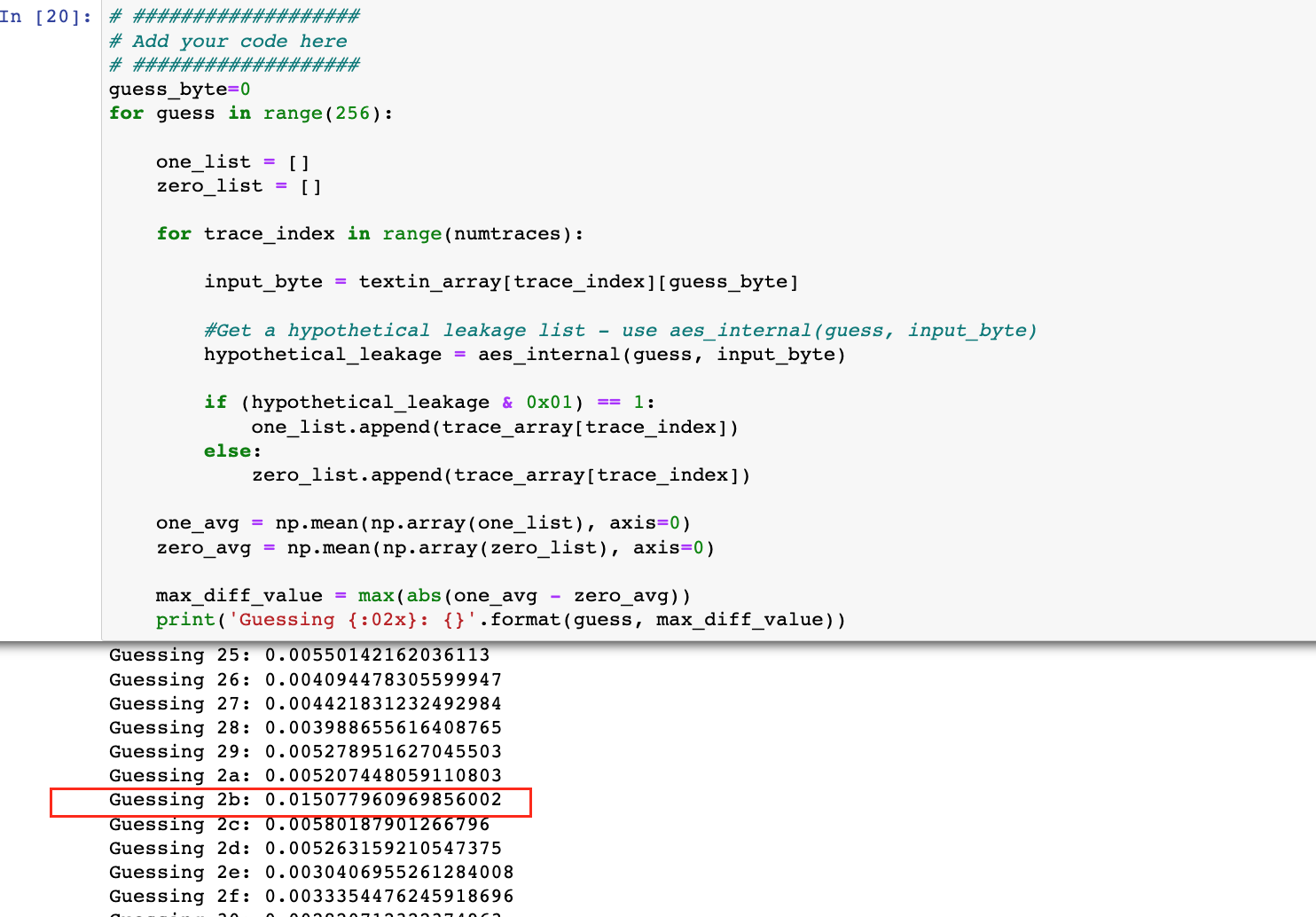
接下来思考，这个方法为什么生效，为什么可以用aes_internal这个函数来划分两个组？
- 可以用aes_internal函数来分组，是因为真正的AES拥有与aes_internal类似的代码片段SubBytes，只不过真正AES还有AddRoundKey、ShiftRows、MixColumns三种操作
- 现在假设用相同密钥key加密2500数据样本，并根据其某一次SubBytes的输出的第0个byte的第0位的值来分成''0"和"1"两组，那么这两组数据所对应的能量迹会有一定的差异（这是前面的知识，指令相同情况下，数据也会对能量消耗产生影响）
- 现在使用aes_internal来对某个key加密的能量迹进行分组，如果猜测的密钥guess是真实值，那么分组结果就恰好是某一次SubBytes的输出的第0个byte的第0位的值'0'和'1'的分组，两组数据会有1个bit的明显差异，那么两者的能量消耗会有比较明显的差异，如果guess不是真实值，那么分组结果的'0'和'1'的两组的数据是随机的，两组数据没有明显差异，两组的能量消耗也就不会有太大差异，这就是这个方法可以生效的原因
接着往下运行，可以看到如下的信息，大意是说：你想要对猜测结果进行排序，这样可以帮助确定最有可能的值。一个最好的方式就是用一个list保存每个猜测的key的最大差异。然后可以使用numpy的argsort来实现排序。
按照上述信息，修改代码后，可以把差异最大的前5的key打印出来，如下图所示
接着可以看到，用来计算差异的函数calculate_diffs
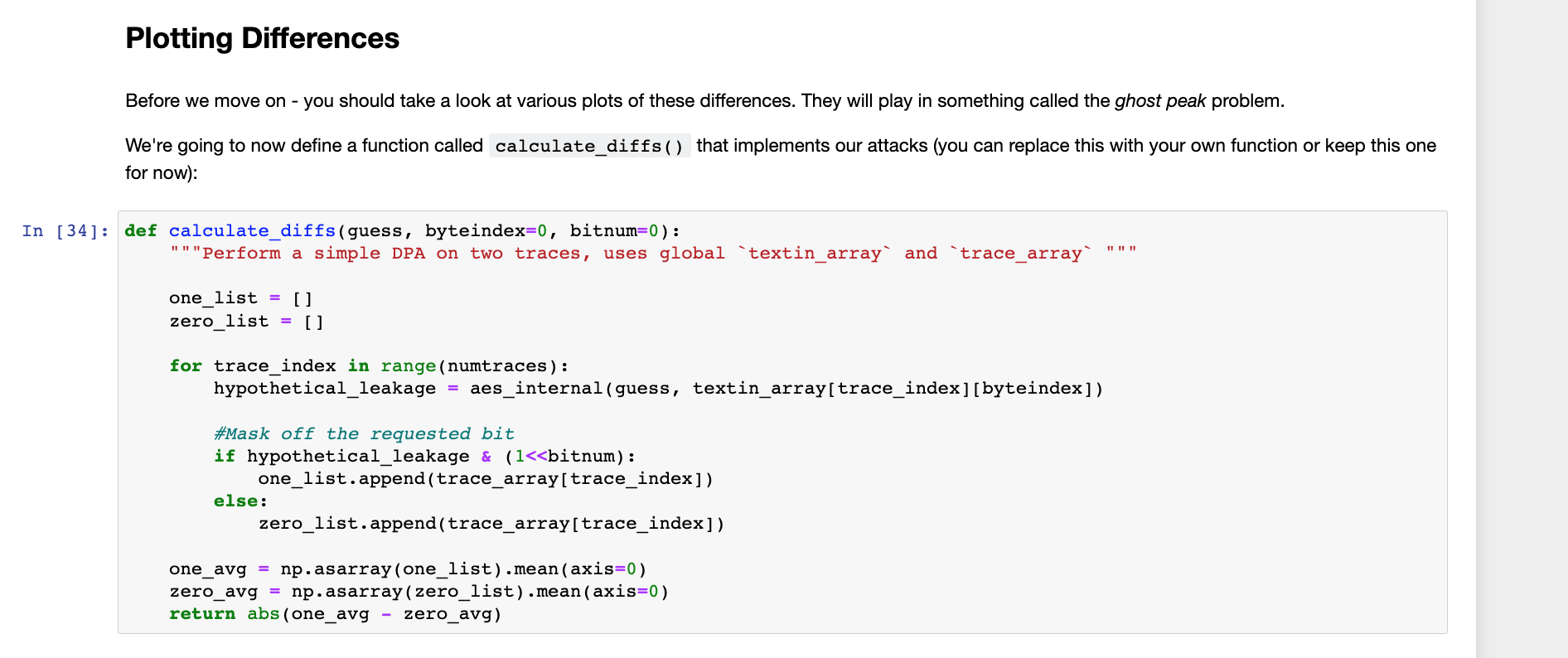
接着按照提示，运行代码，查看画出不同key对应的差异图，这个图的作用就是：既可以直观的看出不同猜测的key造成的差异，又可以看到哪些位置会出现尖峰
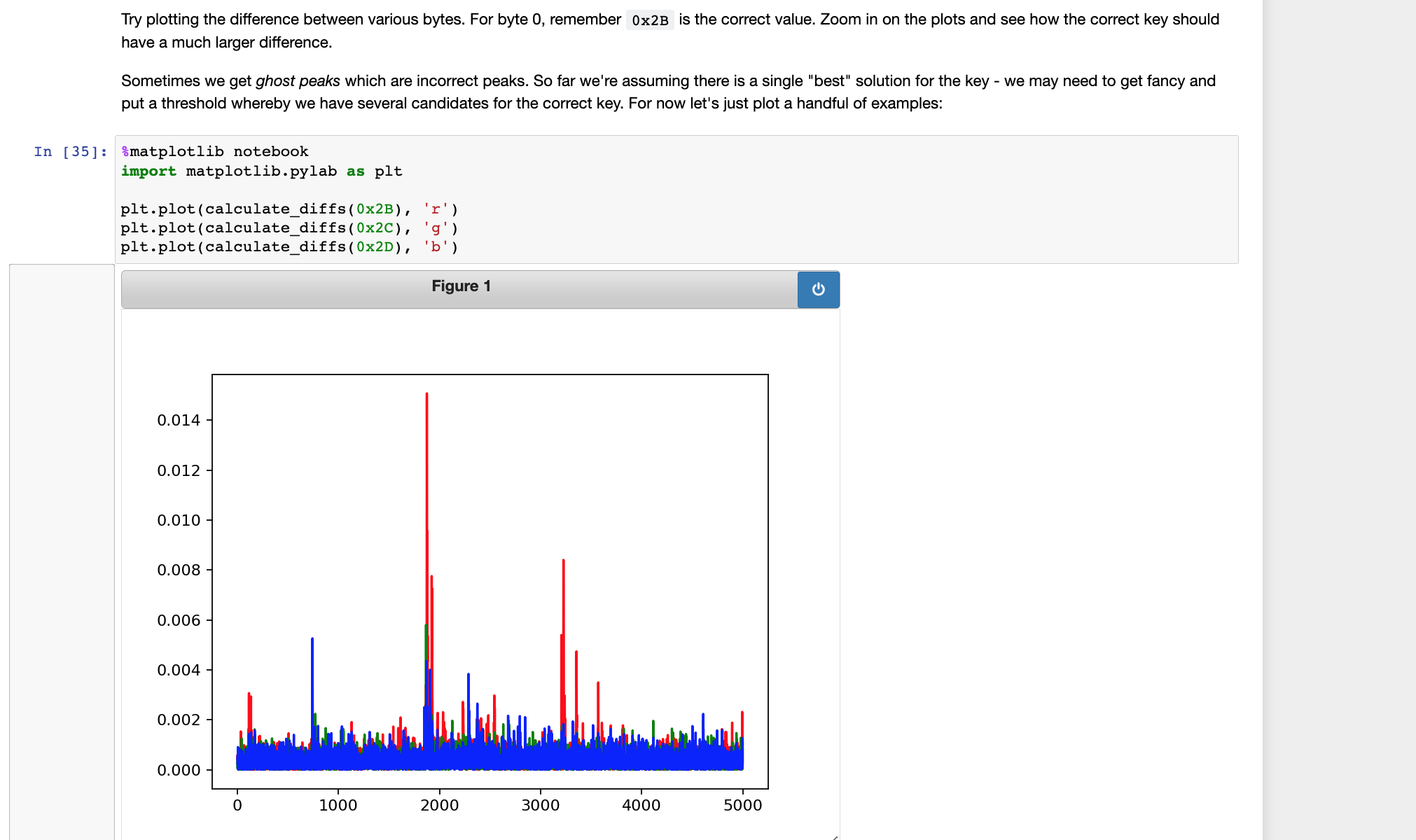
接下来就是根据提示信息，完成自动猜测AES密钥所有字节的代码

补全代码后，运行结果如下图所示，可以看到，猜测正确的寥寥无几（只有第0、5、10个字节这三个是正确），造成这个原因有不少（比如算法实现方式也有关系，如果硬件是CWLITEXMEGA，并且算法选的是AVRCRYPTOLIB，那么这里将直接得到16正确的结果）

from tqdm import tnrange
import numpy as np

#Store your key_guess here, compare to known_key
key_guess = []
known_key = [0x2b, 0x7e, 0x15, 0x16, 0x28, 0xae, 0xd2, 0xa6, 0xab, 0xf7, 0x15, 0x88, 0x09, 0xcf, 0x4f, 0x3c]

for subkey in tnrange(0, 16, desc="Attacking Subkey"):
    max_list=[]
    for guess in range(256):
        max_diff_value = max(calculate_diffs(guess, subkey))
        max_list.append(max_diff_value)
    
    print('Subkey {} - most likelv {:02x} (actual {:02x})'.format(subkey,np.argsort(max_list)[::-1][0], known_key[subkey]))

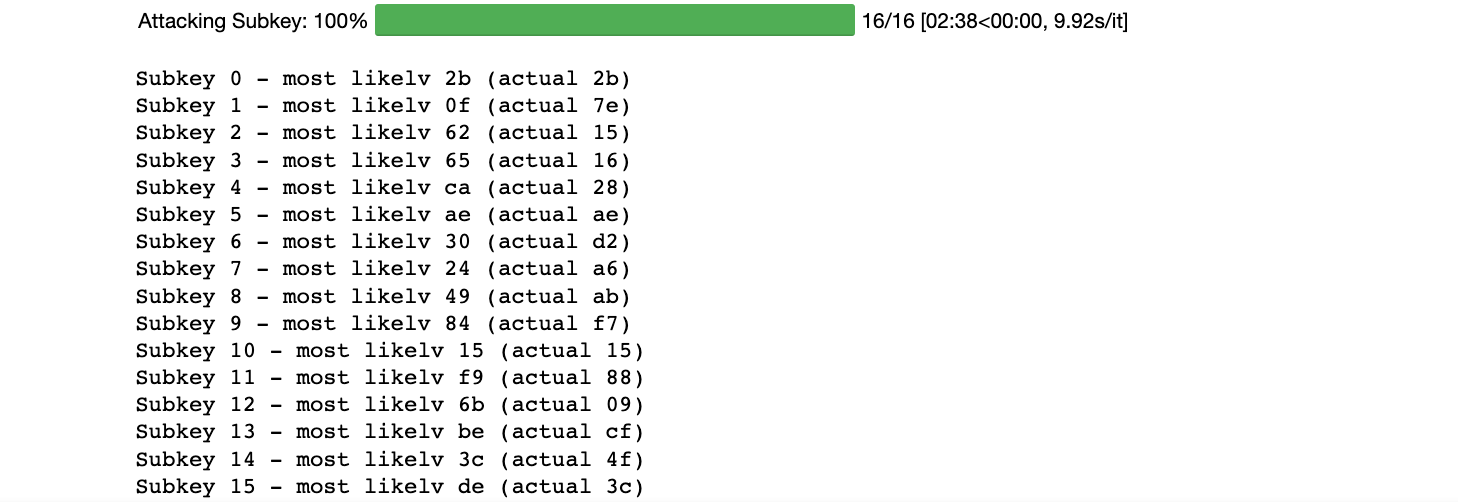
接下来看看教程怎么说这个现象，如下图所示，大意是说：你可能在前面并没有恢复整个密钥？不用担心-造成这个现象是因为有一些其它因素导致的。有一篇关于DPA攻击的文章提到的观点是“你获取了另一个不是正确密钥的强峰（它可能是幽灵峰）”。后面将会有更有效的攻击方法，但是，对于现在，让我们来看一些解决方案：
- 增加抓取的能量迹数量（如将2500变成5000或者10000），增加数据有时就可以解决这个问题了，但有时候真正的幽灵峰可能不会消失，这种情况就需要用其它方法。
- 修改攻击的目标位数（如第'0'位改为第'3'位）或者综合多个位的结果
- 截取数据
接下来就是按照提示信息，运行一个准备好的DPA攻击代码块
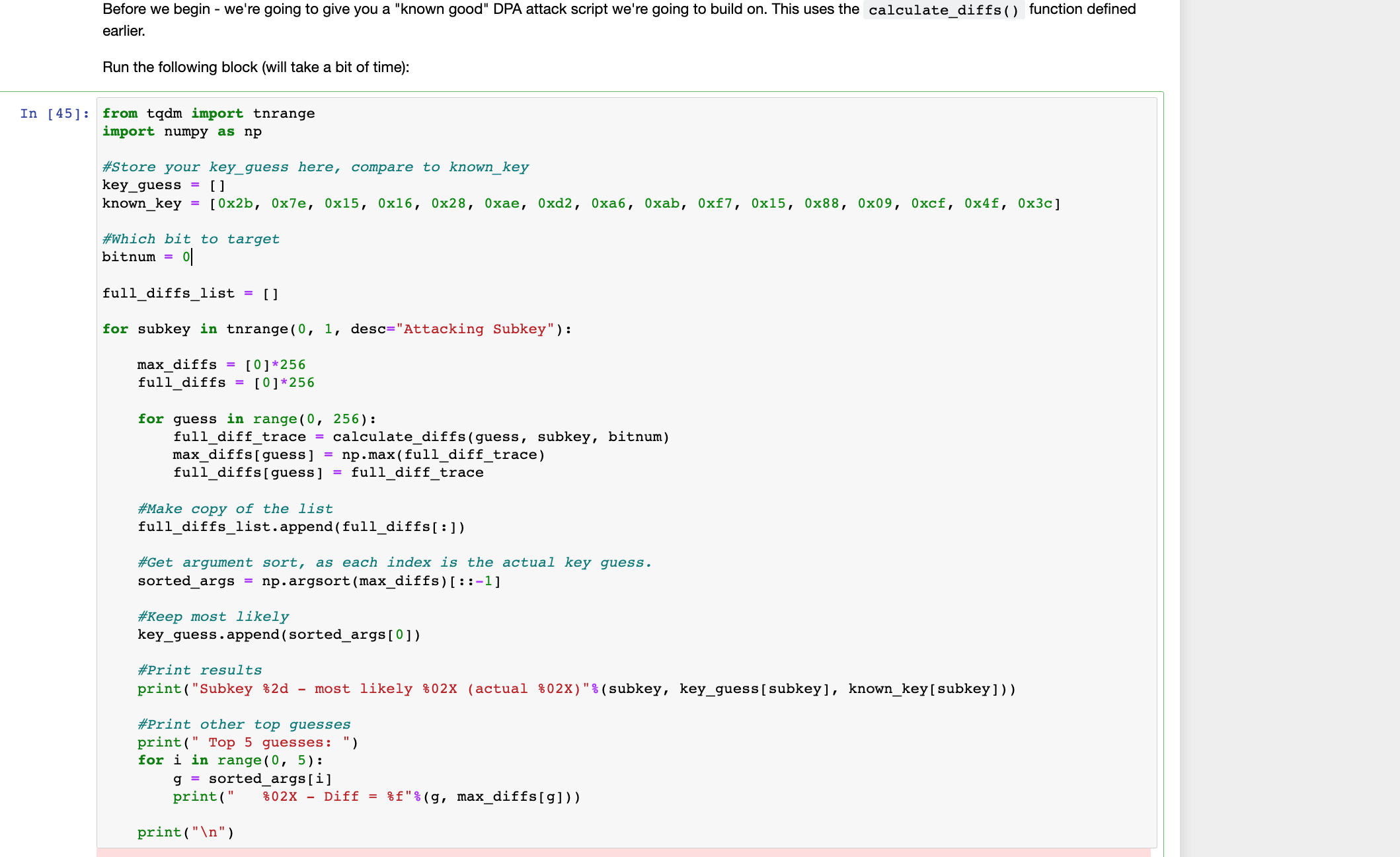
接着就看到如下提示信息，大意是让我们画出猜测错误key的前几个可能值和真实key的差异图
这里因为第5个subkey猜测恰好是正确的（与教程的例子不同），所以选择第1个subkey画图
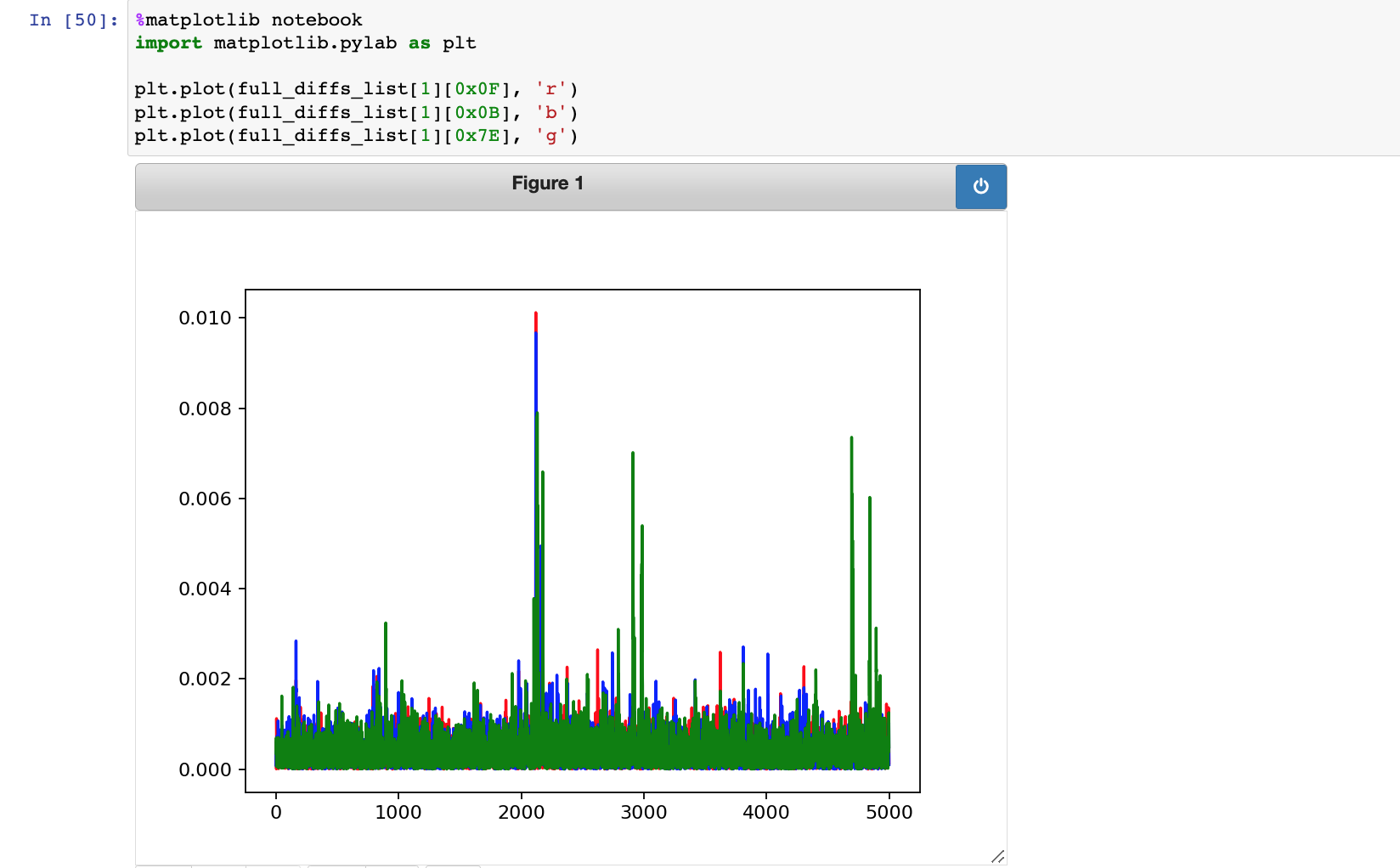
接着看到如下提示信息，大意是说，通过放大你应该可以看到正确key的峰形会在某些地方拥有比错误key的峰形高。从上图看确实如此，在3000和5000附近的位置，正确key的尖峰（绿色）很明显，另外两个的则只在2000附近有一个大的尖峰
然后可以看到如下提示信息，大意是说：取决于你的硬件设备，上图中你会看到一个不错的大尖峰或者多个尖峰。如果有幽灵峰的问题，那么很可能就会有多个尖峰。错误的峰可能与正确的峰错开--所以我们首先可以把所有正确key对应的峰形画出来
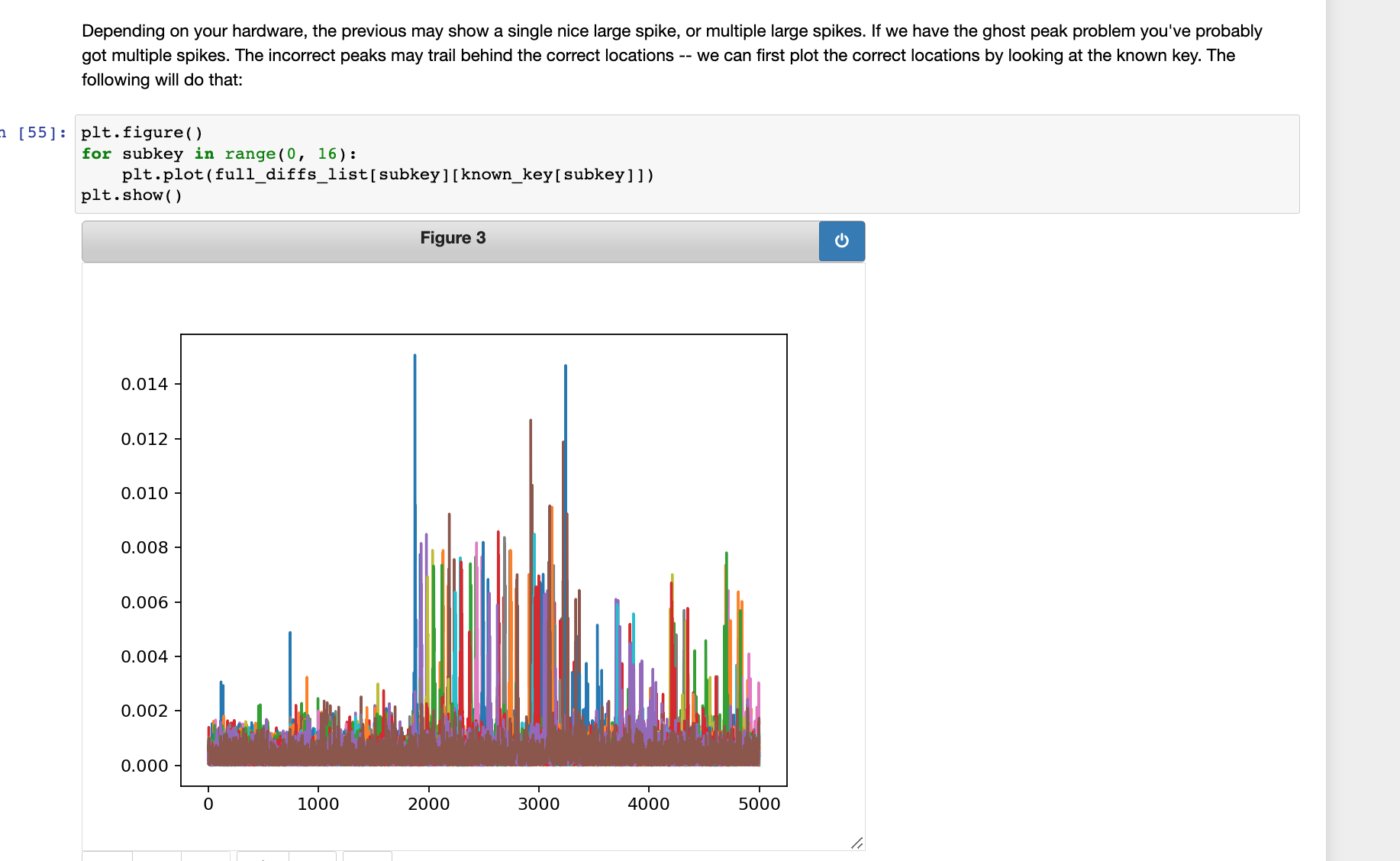
接下来的提示信息是，大意是说：最后一个技巧是 -- 截取数据的一些片段会很有用。例如，从上图可以看到，正确的峰图总是每隔60个周期出现，第一个峰出现在附近1100（这个对于你的硬件可能有所不同）。然后就是提示如何修改代码

最后按照提示做了如下修改，从3220出开始，截取能量迹的数据，这里可以不按每个subkey隔60时钟周期取值，因为实测这样效果更好

from tqdm import tnrange
import numpy as np

#Store your key_guess here, compare to known_key
key_guess = []
known_key = [0x2b, 0x7e, 0x15, 0x16, 0x28, 0xae, 0xd2, 0xa6, 0xab, 0xf7, 0x15, 0x88, 0x09, 0xcf, 0x4f, 0x3c]

#Which bit to target
bitnum = 0

full_diffs_list = []

for subkey in tnrange(0, 16, desc="Attacking Subkey"):
    
    max_diffs = [0]*256
    full_diffs = [0]*256

    for guess in range(0, 256):
        full_diff_trace = calculate_diffs(guess, subkey, bitnum)
        full_diff_trace = full_diff_trace[(3220 + subkey*0):]
        max_diffs[guess] = np.max(full_diff_trace)
        full_diffs[guess] = full_diff_trace
    
    #Make copy of the list
    full_diffs_list.append(full_diffs[:])
    
    #Get argument sort, as each index is the actual key guess.
    sorted_args = np.argsort(max_diffs)[::-1]
    
    #Keep most likely
    key_guess.append(sorted_args[0])
    
    #Print results
    print("Subkey %2d - most likely %02X (actual %02X)"%(subkey, key_guess[subkey], known_key[subkey]))
    
    #Print other top guesses
#     print(" Top 5 guesses: ")
#     for i in range(0, 5):
#         g = sorted_args[i]
#         print("   %02X - Diff = %f"%(g, max_diffs[g]))
    
#     print("\n")

最后运行结果，如下图所示，猜测准确的字节数由原来的3个字节提升到全部字节都猜测正确，不得不说，这个提升很大
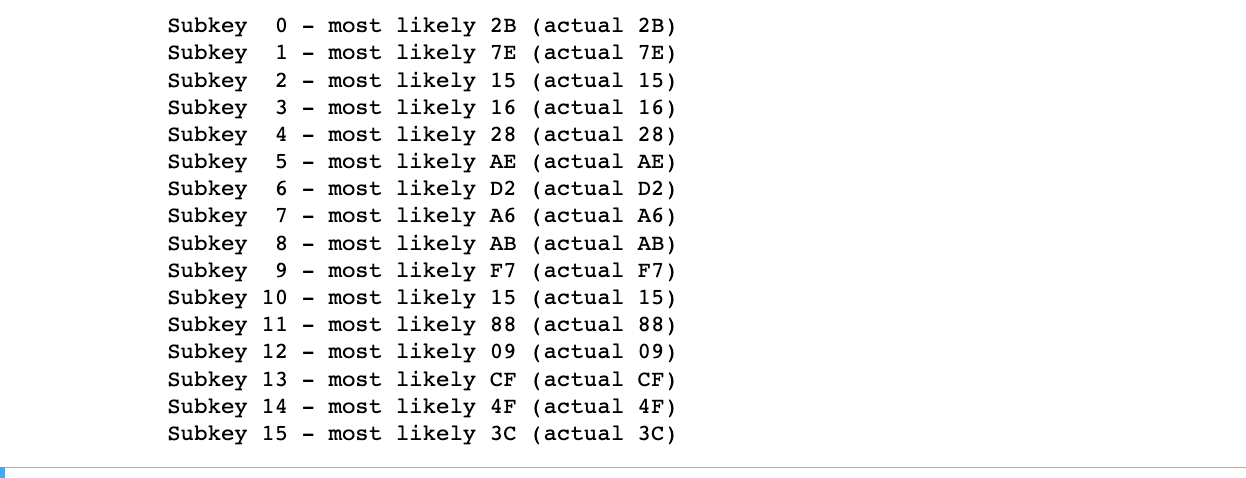
这里解释下为什么从3220的位置开始截取能量迹数据而不是2000附近的位置开始？-- 如下图，因为2000附近的位置除了正确的key会出现尖峰外，错误的key也会出现尖峰，所以需要寻找一个只有正确的key会出现明显尖峰的地方作为数据截取的起始点

总结

学习了如何利用差分能量分析(DPA)来恢复整个AES密钥
了解了幽灵峰的现象，以及一些解决方法